Đáp án C
Cách giải:
M di động luôn nhìn đoạn AB dưới một góc vuông ⇒ M thuộc mặt cầu có một đường kính là AB.
Đáp án C
Cách giải:
M di động luôn nhìn đoạn AB dưới một góc vuông ⇒ M thuộc mặt cầu có một đường kính là AB.
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 1 2 + z - 1 2 = 12 và mặt phẳng (P): x-2y+2z+11=0. Xét điểm M di động trên (P); các điểm A, B, C phân biệt di động trên (S) sao cho AM, BM, CM là các tiếp tuyến của (S). Mặt phẳng (ABC) luôn đi qua điểm cố định nào dưới đây?
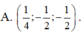
![]()
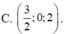
![]()
Trong không gian Oxyz, cho mặt cầu
S : x - 1 2 + y - 2 2 + z - 3 2 = 25 và M(4;5;3). Qua M kẻ các tia Mx, My, Mz đôi một vuông góc với nhau và cắt mặt cầu tại các điểm thứ hai tương ứng là A, B, C. Biết mặt phẳng (ABC) luôn đi qua một điểm cố định H(a;b;c). Tính a+3b-c.
A. 9.
B. 14.
C. 11.
D. 20.
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng ( α ) : 2 x + 2 y + z - 12 = 0 Điểm M di động trên mặt phẳng ( α ) sao cho MA, MB luôn tạo với ( α ) các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn ( ω ) cố định. Hoành độ của tâm đường tròn ( ω ) bằng
A. 9 2
B. 2
C. 10
D. -4
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Cho hai đường thẳng ∆ và ∆ ′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc ∆ và A’ thuộc ∆ ′ . Gọi (P) là mặt phẳng qua A vuông góc với ∆ ′ và d là hình chiếu vuông góc của ∆ trên mặt phẳng (P). Đặt AA’ = a, góc nhọn giữa ∆ và d là α . Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆ ′ lần lượt tại M và M’. Gọi M 1 là hình chiếu vuông góc của M lên mặt phẳng (P).
Khi x thay đổi, tâm O của mặt cầu (S) di động trên đường nào? Chứng minh rằng khi (Q) thay đổi mặt cầu (S) luôn luôn đi qua một đường tròn cố định.
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 1 và điểm A(2;2;2). Xét các điểm M thuộc (S) sao cho đường thẳng AM luôn tiếp xúc với (S). M luôn thuộc một mặt phẳng cố định có phương trình là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 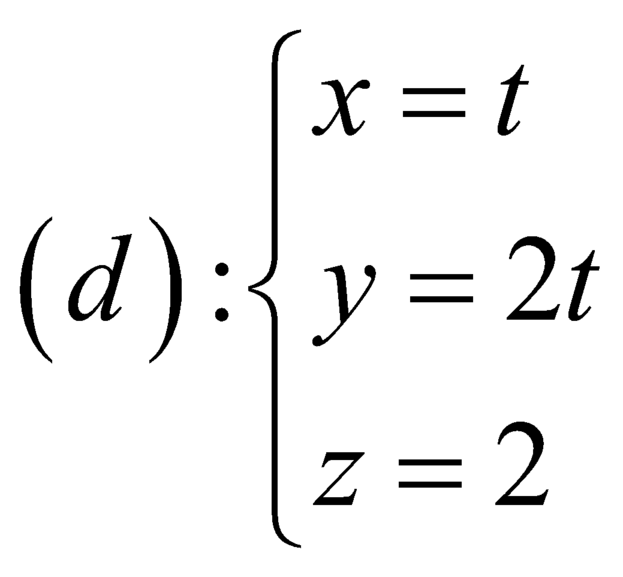
C. 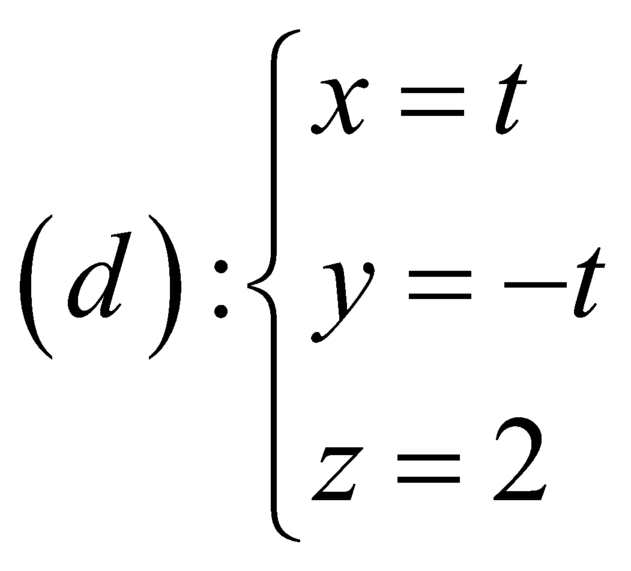
D. 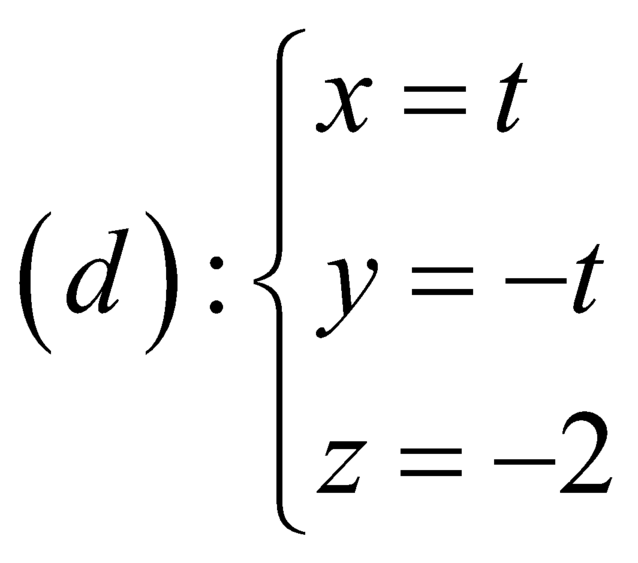 .
.
Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20cm. Gọi d là một đường thẳng thay đổi luôn đi qua A và cách B một khoảng bằng 10cm. Chứng tỏ rằng đường thẳng d luôn nằm trên một mặt nón, hãy xác định mặt nón đó (trục và góc ở đỉnh).
Cho ba điểm A, B, C cùng thuộc một mặt cầu sao cho (ACB)= 90 0 .Trong các khẳng định sau, khẳng định nào đúng?
a) Đường tròn qua ba điểm A, B, C nằm trên mặt cầu.
b) AB là một đường kính của mặt cầu đã cho.
c) AB không phải là đường kính của mặt cầu.
d) AB là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng (ABC).