Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 1 và điểm A(2;2;2). Xét các điểm M thuộc (S) sao cho đường thẳng AM luôn tiếp xúc với (S). M luôn thuộc một mặt phẳng cố định có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng
α
: x+y+z-40 và mặt cầu (S):
x
-
3
2
+
(
y
-
3
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 16 Phương trình đường thẳng α đi qua M và nằm trong α cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng α đi qua điểm nào trong các điểm sau đây?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ^ = 60 o , B M C ^ = 90 o , C M A ^ = 120 o có dạng M(a;b;c) với a<0. Tổng a+b+c bằng:
A. 2
B. -2
C. 1
D. 10 3
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là
(
x
+
5
)
2
+
(
y
-
1
)
2
+
z...
Đọc tiếp
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là ( x + 5 ) 2 + ( y - 1 ) 2 + z 2 = 5 ; x 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 6 và ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 9 . Gọi M là điểm di động ở ngoài ba mặt cầu và X, Y , Z là các tiếp điểm của các tiếp tuyến vẽ từ M đến ba mặt cầu. Giả sử MX = MY = MZ , khi đó tập hợp các điểm M là đường thẳng có vectơ chỉ phương là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²9 và đường thẳng
∆
:
x
-
6
-
3
y
-
2
2
z
-
2
2
. Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) so...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và đường thẳng ∆ : x - 6 - 3 = y - 2 2 = z - 2 2 . Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
A.x-2y+2z-1=0.
B.2x+2y+z-18=0.
C.2x-y-2z-10=0.
D.2x+y+2z-19=0.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
α
)
:
x
+
y
+
z
-
4
0
mặt cầu
(
S
)
:
x
2
+
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) : x + y + z - 4 = 0 mặt cầu ( S ) : x 2 + y 2 + z 2 - 8 x - 6 y - 6 z + 18 = 2 và điểm M(1;1;2) ∈ ( α ) . Đường thẳng d đi qua M nằm trong mặt phẳng ( α ) và cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho dây cung AB có đọ dài nhỏ nhất. Đường thẳng d có một véc tơ chỉ phương là
A. u 1 → = ( 2 ; - 1 ; - 1 )
B. u 3 → = ( 1 ; 1 ; - 2 )
C. u 2 → = ( 1 ; - 2 ; 1 )
D. u 4 → = ( 0 ; 1 ; - 1 )
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
4
x
+
6
y
-
3
0
và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng A. 8. B. 4. C. 2....
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 4 x + 6 y - 3 = 0 và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng
A. 8.
B. 4.
C. 2.
D. 6 5 .
Trong không gian Oxyz cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ⏜ = 60 0 , B M C ⏜ = 90 0 , C M A ⏜ = 120 0 có dạng M(a;b;c) với a<0. Tổng a+b+c bằng:
A. 10 3 .
B. 2.
C. -2.
D. 1.


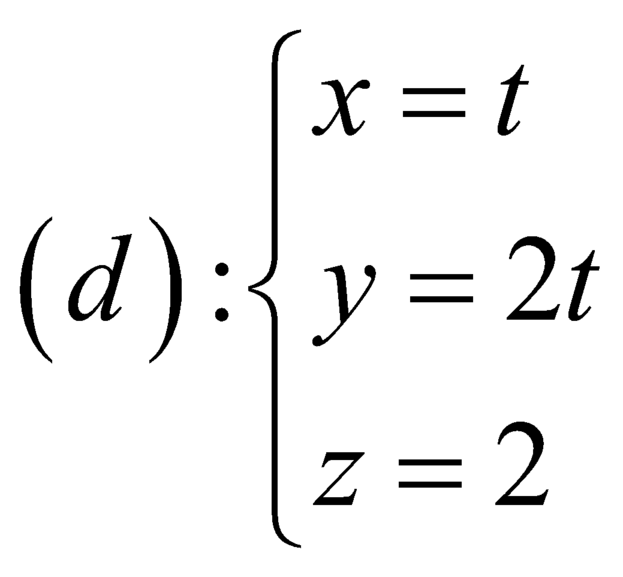
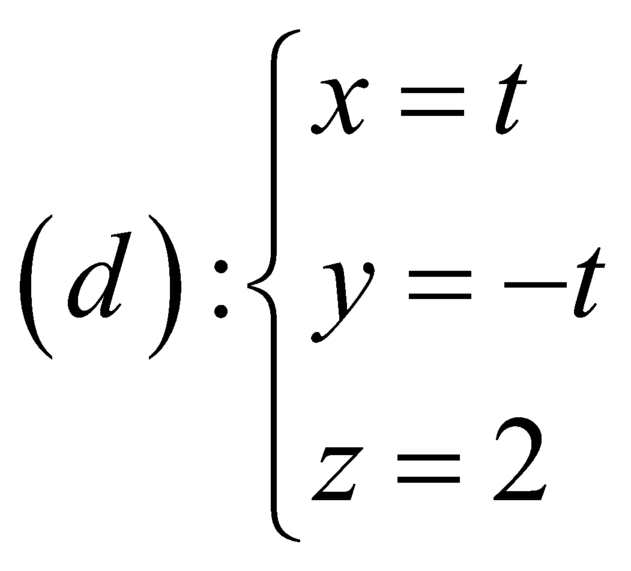
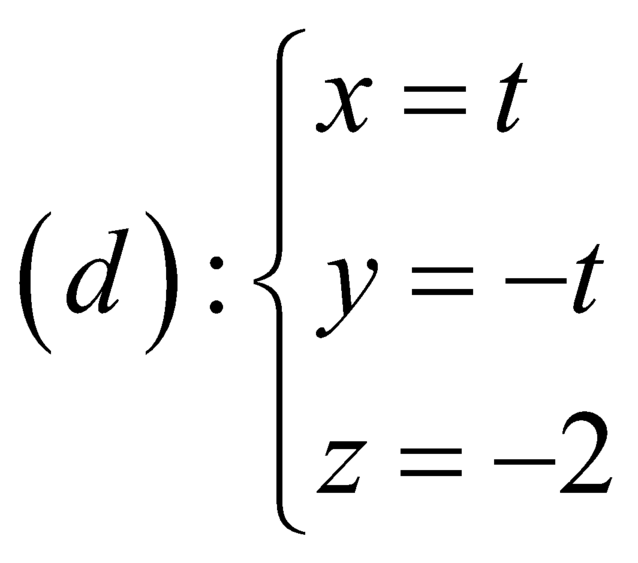 .
.