Đáp án D
Giả sử đồ thị hàm số có dạng y = ax 3 + b x 2 + c x + d
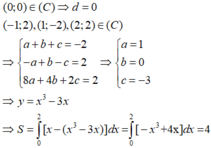
Đáp án D
Giả sử đồ thị hàm số có dạng y = ax 3 + b x 2 + c x + d
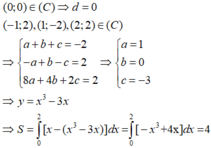
Cho hàm số bậc hai y = f x = x 4 − 5 x 2 + 4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?
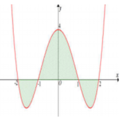
A. S = ∫ − 2 2 f x d x
B. S = 2 ∫ 0 2 f x d x
C. S = 2 ∫ 0 1 f x d x + 2 ∫ 1 2 f x d x
D. S = 2 ∫ 0 2 f x d x
Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y = f x trục hoành và hai đường thẳng x = a ; x = b a < b (phần tô đậm trong hình vẽ) tính theo công thức
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a b f x d x
C. S = ∫ a b f x d x
D. S = − ∫ a c f x d x + ∫ c b f x d x
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f ( x ) = a x 3 + b x 2 + c , các đường thẳng x = - 1 , x = 2 và trục hoành (miền tô đậm) cho trong hình dưới đây
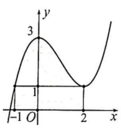
A. S = 51 8
B. S = 52 8
C. S = 50 8
D. S = 53 8
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành, đường thẳng x = a, x = b( như hình bên). Biết ∫ a c f x d x = − 2 v à ∫ c b f x d x = 5 . Hỏi S bằng bao nhiêu?
A. 7
B. 5
C. 2
D. 3
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [ a; b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a , x = b a < b . Diện tích S của hình phẳng D được tính theo công thức
A. S = ∫ a b f x − g x d x
B. S = ∫ a b g x − f x d x
C. S = ∫ a b f x − g x d x
D. S = ∫ a b f x − g x d x
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số y = f 1 x ; y = f 2 x (liên tục trên a , b ) và hai đường thẳng x = a , x = b a < b . Khi đó S được tính theo công thức nào sau đây?
A. S = ∫ a b f 1 x − f 2 x d x .
B. S = ∫ a b f 1 x − f 2 x 2 d x .
C. S = ∫ a b f 1 x − f 2 x d x .
D. S = ∫ a b f 1 x − f 2 x d x .
Cho hình phẳng D giới hạn bởi đồ thị của hai hàm số y=f(x),y=g(x) (phần tô màu như hình vẽ). Gọi S là diện tích hình phẳng D. Mệnh đề nào dưới đây đúng?
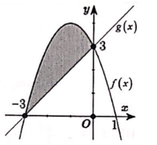
A. S = ∫ - 3 0 [ f ( x ) - g ( x ) ] dx .
B. S = ∫ - 3 0 [ g ( x ) - f ( x ) ] dx .
C. S = ∫ - 3 0 [ f ( x ) + g ( x ) ] dx .
D. S = ∫ - 3 1 [ f ( x ) - g ( x ) ] 2 dx .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π