Đáp án A
Thể tích khối trụ cần tính là V = π R 2 h = π .3 2 .5 = 45 π
Đáp án A
Thể tích khối trụ cần tính là V = π R 2 h = π .3 2 .5 = 45 π
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:
A. r = 10
B. r = 5
C. r = 2
D. r = 15
Cho hình trụ có bán kính đáy r=2a và chiều cao h = a 3 . Tính thể tích V của khối trụ đã cho
A. V = π a 3 3
B. V = 5 π a 3 3
C. V = 2 π a 3 3
D. V = 4 π a 3 3
Thể tích V của khối trụ có bán kính đáy r = 4 và chiều cao h = 4 2 là:
A. V = 32 π
B. V = 32 2 π
C. V = 64 2 π
D. V = 128 π
Tính thể tích V của khối nón có bán kính đáy r = 3 và chiều cao h = 4
A. V = 4 π
B. V = 12 π
C. V = 16 π 3
D. V = 4
Cho khối nón có bán kính đáy r = 3, chiều cao h = 2 Tính thể tích V của khối nón.
A. V = 3 π 2 3
B. V = 3 π 2
C. V = 9 π 2 3
D. V = 9 π 2
Cho hình trụ có bán kính đáy bằng a và chiều cao bằng h. Tính thể tích V của khối lăng trụ tam giác đều nội tiếp hình trụ đã cho.
A. V = 3 a 2 h 4
B. V = 3 3 a 2 h 4
C. V = π 3 h 2 + 4 a 2 3 h 2 4 + a 2 3
D. V = 3 3 π a 2 h 4
Một khúc gỗ có dạng khối nón có bán kính đáy r= 30 km, chiều cao h= 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
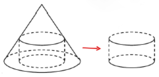
A. V = 0 , 16 m 3
B. V = 0 , 024 m 3
C. V = 0 , 027 m 3
D. V = 0 , 016 m 3
Một khúc gỗ có dạng khối nón có bán kính đáy r = 30cm, chiều cao h = 120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ.
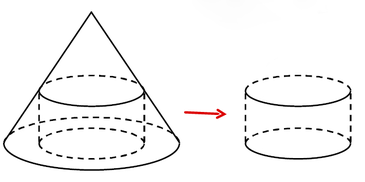
Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V.
A. V = 0 , 16 π m 3 .
B. V = 0 , 024 π m 3 .
C. V = 0 , 36 π m 3 .
D. V = 0 , 016 π m 3 .