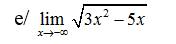\(\lim\limits_{x\rightarrow-\infty}\sqrt{3x^2-5x}\)
\(=\lim\limits_{x\rightarrow-\infty}\sqrt{x^2\left(3-\dfrac{5}{x}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}-x\cdot\sqrt{3-\dfrac{5}{x}}\)
\(=-\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}-x=+\infty\\\lim\limits_{x\rightarrow-\infty}\sqrt{3-\dfrac{5}{x}}=\sqrt{3}>0\end{matrix}\right.\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\dfrac{-n^2+2n+1}{\sqrt{3n^4+2}}\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{4n-\sqrt{16n^2+1}}{n+1}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{\sqrt{9n^2+n+1}-3n}{2n}\right)\)
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4.2^{n+1}-3}{3.2^n+4^n}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{2-5^{n-2}}{3^n+2.5^n}\right)\)
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\sqrt{n^2-1}+3n\)
2) tính giới hạn I = \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+5}+n\right)\)
1. hàm số y = 3cosx luôn nhận giá trị trong tập nào
2. tập xác định của hàm số y = cosx
3. tính giới hạn \(L=\lim\limits\dfrac{n^2-3n^3}{2n^3+5n-2}\)
4. tính giới hạn \(L=\lim\limits\left(3n^2+5n-3\right)\)
5. kết quả của giới hạn \(\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\)
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n^2+6n}-n\right)\)
2) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n+1}-\sqrt{n-1}\right)\)
Tính giới hạn
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{7^n+2^2}{3.7^n+4^n}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{1-4^n}{1+4^n}\right)\)
Tính giới hạn A= l i m 1 n ?
A.0
B.1
C.2
D.3
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt[3]{n^3+3n^2+1}-n\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+1}-\sqrt[3]{8n^3+n}\right)\)
