Các câu hỏi tương tự
Đạo hàm của hàm số
y
x
+
1
.
ln
x
là: A.
y
x
ln
x
+
2
x
+
1
2...
Đọc tiếp
Đạo hàm của hàm số y = x + 1 . ln x là:
A. y ' = x ln x + 2 x + 1 2 x x + 1 .
B. y ' = 1 2 x x + 1 .
C. y ' = x + x + 1 x x + 1 .
D. y ' = 3 x + 2 2 x x + 1 .
Đạo hàm của hàm số
y
ln
x
+
x
2
+
1
A.
y
2
x
x
+
x
2
+
1...
Đọc tiếp
Đạo hàm của hàm số y = ln x + x 2 + 1
A. y ' = 2 x x + x 2 + 1
B. y ' = 1 + 2 x 2 x 2 + 1
C. y ' = 1 x 2 + 1
D. y ' = 1 x + x 2 + 1
Tính đạo hàm của hàm số
y
ln
x
-
1
x
+
2
A.
y
-
3
(
x
-
1
)
(
x
+...
Đọc tiếp
Tính đạo hàm của hàm số y = ln x - 1 x + 2
A. y ' = - 3 ( x - 1 ) ( x + 2 ) .
B. y ' = - 3 ( x - 1 ) ( x + 2 ) 2 .
C. y ' = 3 ( x - 1 ) ( x + 2 ) .
D. y ' = - 3 ( x - 1 ) ( x + 2 ) 2 .
Hàm số y lnx + 1/x là nguyên hàm của hàm số nào dưới đây? A. Y ln + 1 B.
y
1
x
-
1
x
2
C.
y
1
2
ln
2
x
-
1
x
2
D. ...
Đọc tiếp
Hàm số y = lnx + 1/x là nguyên hàm của hàm số nào dưới đây?
A. Y = ln + 1
B. y = 1 x - 1 x 2
C. y = 1 2 ln 2 x - 1 x 2
D. y = 1 2 ln 2 x - 1 x
Đạo hàm của hàm số
y
ln
x
+
x
2
là A.
y
1
x
+
x
B.
y
1
x
+
2
x
.
C.
y...
Đọc tiếp
Đạo hàm của hàm số y = ln x + x 2 là
A. y ' = 1 x + x
B. y ' = 1 x + 2 x .
C. y ' = 1 x − 2 x .
D. y ' = 1 x + x 3 3 .
Cho hàm số
y
e
x
+
ln
x
Tính y (1) A.
y
(
1
)
e
+
1
B.
y
(
1
)
e
+
3
C.
y
(
1
)
e
-
1
D.
y
(
1
)...
Đọc tiếp
Cho hàm số y = e x + ln x Tính y' (1)
A. y ' ( 1 ) = e + 1
B. y ' ( 1 ) = e + 3
C. y ' ( 1 ) = e - 1
D. y ' ( 1 ) = e - 3
Hàm số ylnx có đạo hàm cấp n là A.
n
!
x
n
B.
(
-
1
)
n
+
1
(
n
-
1
)
!
x...
Đọc tiếp
Hàm số y=lnx có đạo hàm cấp n là
A. n ! x n
B. ( - 1 ) n + 1 ( n - 1 ) ! x n
C. 1 x n
D. n ! x n + 1
Đạo hàm của
y
ln
x
+
x
2
-
1
là: A.
y
x
x
2
-
1
B.
y
-
1
x...
Đọc tiếp
Đạo hàm của y = ln x + x 2 - 1 là:
A. y ' = x x 2 - 1
B. y ' = - 1 x 2 - 1
C. y ' = 1 x 2 - 1
D. y ' = 1 2 x 2 - 1
Cho hàm số y f(x). Hàm số y f’(x) có đồ thị như hình vẽ. Hàm số y f(lnx +1) nghịch biến trên khoảng A. (e;+∞). B. (1/e;e). C.
1
e
3
;
1
e
D.(0;e)
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f’(x) có
đồ thị như hình vẽ. Hàm số y = f(lnx +1) nghịch biến
trên khoảng
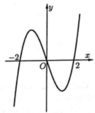
A. (e;+∞).
B. (1/e;e).
C. 1 e 3 ; 1 e
D.(0;e)
Cho hàm số yf(x) Hàm số yf’(x) có đồ thị như hình vẽ. Hàm số yf(-lnx+1) nghịch biến trên khoảng A. (e;+∞) B. (1/e;e) C.
1
e
3
;
e
D. (0;e)
Đọc tiếp
Cho hàm số y=f(x) Hàm số y=f’(x) có đồ thị như hình vẽ. Hàm số y=f(-lnx+1) nghịch biến trên khoảng
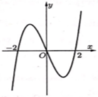
A. (e;+∞)
B. (1/e;e)
C. 1 e 3 ; e
D. (0;e)



