Các câu hỏi tương tự
Cho hàm số yf(x) xác định và liên tục trên [1;e] thỏa mãn
xf
(
x
)
x
[
f
(
x
)
]
2
+
3
f
(
x
)
+
4
x
và f(1) -3. Tính f(e). A.
5
2
e
B. -...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho các phát biểu sau(1) Đơn giản biểu thức
M
a
1
4
-
b
1
4
a
1
4
+
b
1...
Đọc tiếp
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Cho hàm số
y
2
ln
ln
x
-
ln
2
x
. Tính giá trị của y(e) A.
1
e
B.
2
e
C.
e
2
D.
1
2
e
Đọc tiếp
Cho hàm số y = 2 ln ln x - ln 2 x . Tính giá trị của y'(e)
A. 1 e
B. 2 e
C. e 2
D. 1 2 e
Giá trị nhỏ nhất của hàm số y = ln x x trên đoạn [1;e] bằng:
A. 0
B. 1
C. - 1 e
D. e
Cho hàm số
y
f
(
x
)
2019
l
n
e
x
2019
+
e
. Tính giá trị biểu thức
A
f
’
(
1
)
+...
Đọc tiếp
Cho hàm số y = f ( x ) = 2019 l n e x 2019 + e . Tính giá trị biểu thức A = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2018 )
A. 2018
B. 1009
C. 2017 2
D. 2019 2
Cho hàm số \(y=x^3+3x^2+mx+1\)\(\left(C_m\right)\)
Tìm m để \(\left(C_m\right)\) cắt đường thẳng y=1 tại 3 điểm phân biệt C (0;1), D, E. Tìm m để các tiếp tuyến tại D, E vuông góc với nhau
CHO x;y thuộc Z và x;y khác 0
thỏa mãn \(\frac{x^2}{y^2}+\frac{y^2}{x^2}+2\left(x+y\right)-3\left(\frac{x}{y}+\frac{y}{x}\right)+3\left(\frac{1}{x}+\frac{1}{y}\right)-\frac{2}{xy}=4\)
TÍNH E=x+y
Cho hàm số yf(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) (3x2+2x)e-f(x)
∀
x
∈
-
1
;
0
Tính giá trị biểu thức Af(0)-f(-1)
Đọc tiếp
Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x2+2x)e-f(x) ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1)
![]()
![]()
![]()
![]()
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
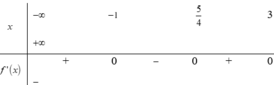
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho hàm số
y
e
a
x
2
+
b
x
+
c
đạt cực trị tại x1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x2? A.
y
2
e
2
B.
y
2...
Đọc tiếp
Cho hàm số y = e a x 2 + b x + c đạt cực trị tại x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x=2?
A. y 2 = e 2
B. y 2 = 1 e 2
C. y 2 = 1
D.. y 2 = e






