Đáp án C
Với y = x 2 − 1 ⇒ d u = 2 x d x .
Vậy I = ∫ u d u .
Đáp án C
Với y = x 2 − 1 ⇒ d u = 2 x d x .
Vậy I = ∫ u d u .
Câu 1:(0,5đ)
Liệt kê các phần tử của tập hợp A = {x ∈ N/15 ≤ x ≤ 19}
Câu 2: (3đ) thực hiện phép tính
a. 2.(72 – 2.32) – 60
b. 27.63 + 27.37
c. l-7l + (-8) + l-11l + 2
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
Câu 3: ( 2,5 điểm ) Tìm số nguyên x
a) 2x + 3 = 52 : 5
b) 105 – ( x + 7) = 27 : 25
Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.
Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ hình minh họa.
Câu 6: ( 2 điểm )Vẽ tia Ox, trên Ox lấy điểm A và B sao cho OA= 4cm, OB = 8cm.
a. Trong 3 điểm O, A, B điểm nào nằm giữa 2 điểm còn lại. Vì sao? . So sánh OA và AB
b. A có phải là trung điểm của OB không? Vì sao ?
Tính tích phân I = ∫ 0 π x 2 cos 2 2 xdx bằng cách đặt u = x 2 d v = cos 2 x dx . Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x 0 π - ∫ 0 π x sin 2 xdx
B. I = 1 2 x 2 sin 2 x 0 π - 2 ∫ 0 π x sin 2 xdx
C. I = 1 2 x 2 sin 2 x 0 π + 2 ∫ 0 π x sin 2 xdx
D. I = 1 2 x 2 sin 2 x 0 π + ∫ 0 π x sin 2 xdx
Tính tích phân I = ∫ 0 π x 2 c o s 2 2 x d x bằng cách đặt u = x 2 d v = c o s 2 x d x . Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x π 0 − ∫ 0 π x sin 2 x d x .
B. I = 1 2 x 2 sin 2 x π 0 − 2 ∫ 0 π x sin 2 x d x .
C. I = 1 2 x 2 sin 2 x π 0 + 2 ∫ 0 π x sin 2 x d x .
D. I = 1 2 x 2 sin 2 x π 0 + ∫ 0 π x sin 2 x d x .
Tính tích phân I = ∫ 0 π x 2 cos 2 2 x d x bằng cách đặt u = x 2 d v = cos 2 x d x
Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x 0 π - ∫ 0 π x sin 2 x d x
B. I = 1 2 x 2 sin 2 x 0 π - 2 ∫ 0 π x sin 2 x d x
C. I = 1 2 x 2 sin 2 x 0 π + 2 ∫ 0 π x sin 2 x d x
D. I = 1 2 x 2 sin 2 x 0 π + ∫ 0 π x sin 2 x d x
Trong không gian Oxyz, cho đường thẳng d: x - 2 1 = y - 1 - 2 = z - 1 2 và hai điểm A(3;2;1), B(2;0;4). Gọi ∆ là đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến ∆ là nhỏ nhất. Gọi u → = 2 ; b ; c là một VTCP của ∆. Khi đó , u → bằng
A. 17
B. 5
C. 6
D. 3
Cho hàm số y = f(x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ α ; β ] ∀ x ∈ [ a ; b ] hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A. ∫ a b f ( u ( x ) ) u ' d x = ∫ u ( a ) u ( b ) f ( u ) d u
B. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
C. ∫ u ( a ) u ( b ) f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
D. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( x ) d x
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1.
B. 2
C. 3
D. 4.
Cho I = 1 2 ∫ 0 4 x 1 + 2 x d x và u = 2 x + 1 . Mệnh đề nào dưới đây sai?
A. I = 1 2 ∫ 1 3 x 2 x 2 − 1 d x
B. I = ∫ 1 3 u 2 u 2 − 1 d u
C. I = 1 2 u 5 5 − u 3 3 1 3
D. I = 1 2 ∫ 1 3 u 2 u 2 − 1 d u
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
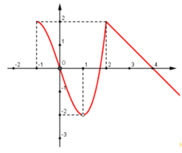
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3