Question

Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: g(x) = | x 3 + 3 x 2  – 72x + 90| trên đoạn [-5; 5]

Answer 1

Xét hàm số f(x) =  x 3  + 3 x 2  − 72x + 90 trên đoạn [-5;5]

f′(x) =3 x 2  + 6x − 72;

f′(x) = 0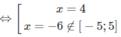 

f(−5) = 400; f(5) = −70; f(4) = −86

Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x 0   ∈ (−5;5) sao cho f( x 0 ) = 0

Ta có g(x) = |f(x)| ≤ 0 và g( x 0 ) = |f( x 0 )| = 0;

g(−5) = |400| = 400

g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86

Vậy min g(x) = g( x 0 ) = 0; max g(x) = g(−5) = 400