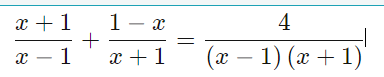\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\left(ĐKXĐ:x\ne1;x\ne-1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x+1\right)+\left(1-x\right)\left(x-1\right)=4\)
\(\Leftrightarrow x^2+x+x+1+x-1-x^2+x=4\)
\(\Leftrightarrow x^2-x^2+x+x+x+x-4+1-1=0\)
\(\Leftrightarrow4x-4=0\)
\(\Leftrightarrow4x=4\)
\(\Leftrightarrow x=1\left(loại\right)\)
Vậy \(S=\varnothing\)
\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(1-x\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1+x-1\right)\left(x+1-x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{2x.2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{4x}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇒ \(4x=4\)
⇔ \(x=1\) (ko thỏa mãn dktc)
Vậy phương trình vô nghiệm