Các câu hỏi tương tự
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a 5b 15-c. Tìm giá trị nhỏ nhất của biểu thức P a2 + b2 + c2 - 4(a+b+c)
Đọc tiếp
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a = 5b = 15-c. Tìm giá trị nhỏ nhất của biểu thức P = a2 + b2 + c2 - 4(a+b+c)
![]()
![]()
![]()
![]()
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất
A. 13 và 0 B. 13/2 và -13/2
C. 15 và 2 D. 30 và 15
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất
A. 13 và 0 B. 13/2 và -13/2
C. 15 và 2 D. 30 và 15
Biết các số thực a,b thỏa mãn:
0
b
a
≤
2
và
2
a
b
≤
2
b
+
a
Tìm giá trị lớn nhất của F
a
2
+
b
2
Đọc tiếp
Biết các số thực a,b thỏa mãn: 0 < b < a ≤ 2 và 2 a b ≤ 2 b + a Tìm giá trị lớn nhất của F= a 2 + b 2
![]()
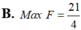
![]()
![]()
Cho các số thực a; b; c và d thỏa mãn: a+ bi ( c+ di) n. Tìm khẳng định đúng A. a2 + b2 2( c2 + d2) n B. a2 + b2 c2 + d2 C. a2 + b2 2n( c2 + d2) D. a2 + b2 ( c2 + d2)n
Đọc tiếp
Cho các số thực a; b; c và d thỏa mãn: a+ bi= ( c+ di) n. Tìm khẳng định đúng
A. a2 + b2 = 2( c2 + d2) n
B. a2 + b2 = c2 + d2
C. a2 + b2 = 2n( c2 + d2)
D. a2 + b2 = ( c2 + d2)n
Nếu a, b là các số nguyên dương thỏa mãn a/4b = 6.35. Số nào dưới đây có thể là số dư khi 4a chia cho 2b i. 10 ii. 20 iii. 40 A. chỉ I B. chỉ II C. chỉ III D. I và II E. I, II và III
Cho 2 số thực dương x,y thỏa mãn {left( {x + y} right)^3} + x + y + {log _2}dfrac{{x + y}}{{1 - xy}} 8{left( {1 - xy} right)^3} - 2xy + 3 Tính giá trị nhỏ nhất của biểu thứP x + 3yA. dfrac{{1 + sqrt {15} }}{2}.B. dfrac{{3 + sqrt {15} }}{2}.C.sqrt {15} - 2.D. dfrac{{3 + 2sqrt {15} }}{6}.
Đọc tiếp
Cho 2 số thực dương x,y thỏa mãn \({\left( {x + y} \right)^3} + x + y + {\log _2}\dfrac{{x + y}}{{1 - xy}} = 8{\left( {1 - xy} \right)^3} - 2xy + 3\) Tính giá trị nhỏ nhất của biểu thứ
P = x + 3y |
A. \(\dfrac{{1 + \sqrt {15} }}{2}.\)
B. \(\dfrac{{3 + \sqrt {15} }}{2}.\)
C.\(\sqrt {15} - 2.\)
D. \(\dfrac{{3 + 2\sqrt {15} }}{6}.\)
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho a, b là các số thực dương thỏa mãn
a
≠
1
,
a
≠
b
và
log
a
b
2
. Tính
P
log
b
a
a
b
Đọc tiếp
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b