Đáp án: B.
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích p(x) = x(x + 13) = x 2 + 13x;
p'(x) = 2x + 13; p'(x) = 0 ⇔ x = -13/2.
Bảng biến thiên
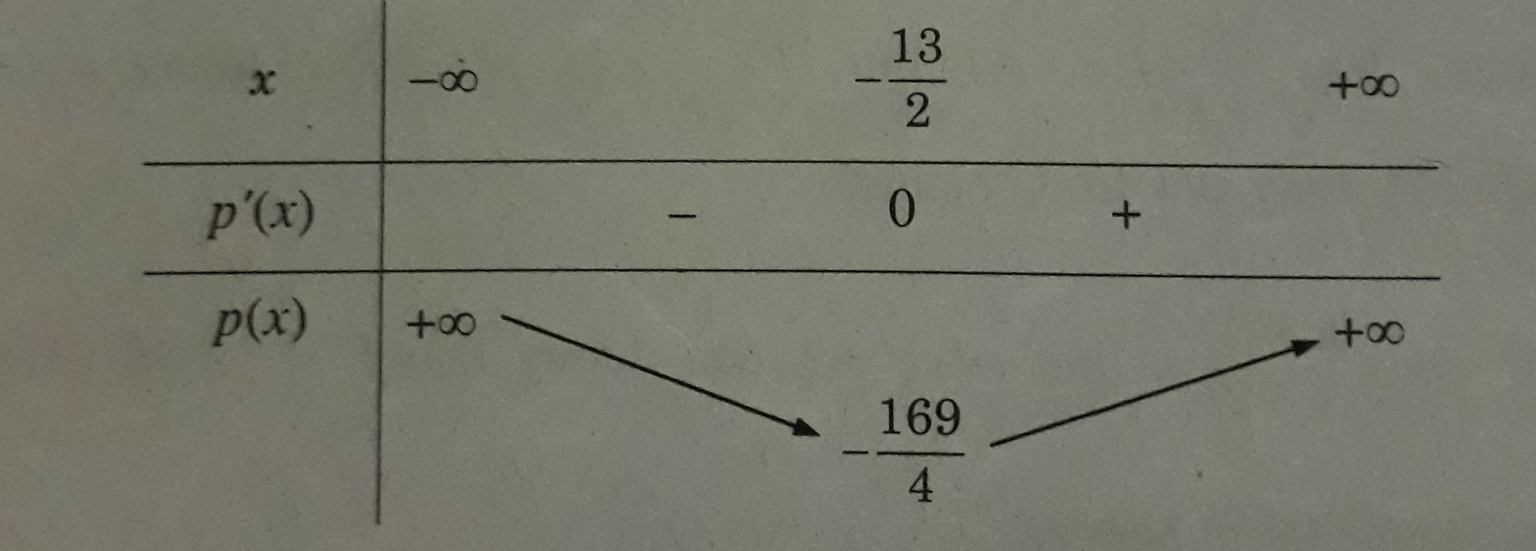
Vậy tích hai số là bé nhất khi một số là x = -13/2 và số kia là x + 13 = 13/2.
Đáp án: B.
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích p(x) = x(x + 13) = x 2 + 13x;
p'(x) = 2x + 13; p'(x) = 0 ⇔ x = -13/2.
Bảng biến thiên
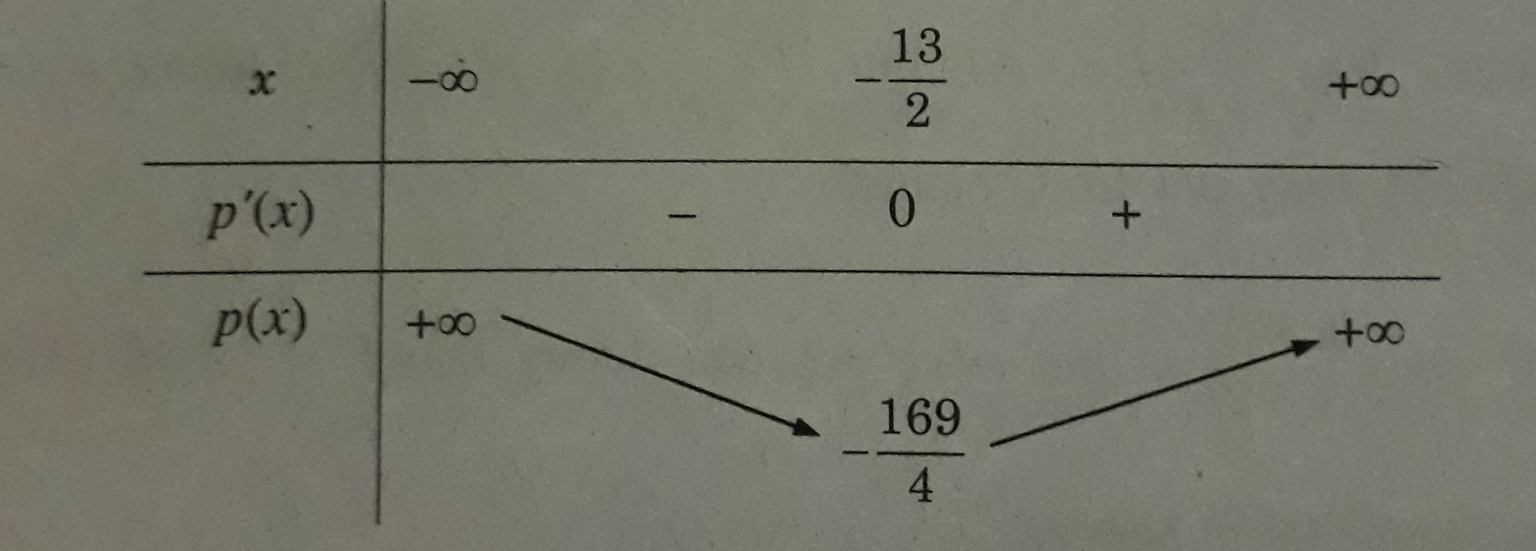
Vậy tích hai số là bé nhất khi một số là x = -13/2 và số kia là x + 13 = 13/2.
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất
A. 13 và 0 B. 13/2 và -13/2
C. 15 và 2 D. 30 và 15
Cho d : x + 2 1 = y - 1 3 = z + 5 - 2 và A(-2;1;1), B(-3;-1;2). Gọi M là điểm thuộc đường thẳng d sao cho tam giác AMB có diện tích 3 5 . Tìm tọa độ điểm M.
![]()
![]()
![]()
![]()
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm
A', B', C' sao cho SA' = 1 3 SA , SB' = 1 3 SB, SC' = 1 3 SC. Gọi V và V'
lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là
![]()
![]()
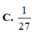
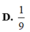
Gọi z 1 ; z 2 là hai nghiệm của phương trình z 2 - 4 z + 13 = 0 và A; B lần lượt là hai điểm biểu diễn cho hai số phức z 1 ; z 2 , trong mặt phẳng tọa độ Oxy. Diện tích tam giác OAB bằng
A. 13
B. 12
C. 13 2
D. 6
Đường thẳng d song song với hai mặt phẳng
(P): 3x + 12y - 3z - 5 = 0,
(Q): 3x - 4y + 9z = 0 và đồng thời cắt
cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 : x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 v à ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng ∆1;∆2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t