Phương pháp:
+) Tìm tọa độ các điểm cực trị của đồ thị hàm số theo tham số m.
+) Dựa vào tính chất hàm trùng phương và tính chất tứ giác nội tiếp để tìm m.
Cách giải:
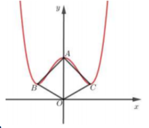
Tìm tập hợp S tất cả các giá trị của tham số m để đồ thị hàm số y = x 4 − 2 m 2 x 2 + m 4 + 3 có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành tứ giác nội tiếp
A. S = − 1 3 ; 0 ; 1 3
B. S = − 1 ; 1
C. S = − 1 3 ; 1 3
D. S = − 1 2 ; 1 2
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số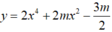 
có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
B. -3
C. -1
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 + 2 m x 2 − 3 m 2 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S
A. 2 − 2 3
B. − 2 − 2 3
C. − 1
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 + 2 m x 2 − 3 m 2 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
A. 2 − 2 3 .
B. − 2 − 3 .
C. -1.
D. 0.
Gọi S là tập hợp tất cả các giá trị của tham số m đồ thị (C) của hàm số y = x 4 − 2 m 2 x 2 + m 4 + 5 có ba cực trị, đồng thời ba điểm cực trị với gốc tọa độ tạo thành một tứ giác nội tiếp. Tìm số phần tử của S.
A. 3
B. 2
C. 1
D. 0
Tìm các giá trị của tham số m để đồ thị hàm số y = x 4 - 2 m x 2 + m có 3 điểm cực trị. Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hớn 1.
A. m < -1
B. m > 2 hoặc m < -1
C. m > 2
D. m > 0
Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m 2 + 2 có ba điểm cực trị cùng với điểm D(2;1) tạo thành một tứ giác nội tiếp được đường tròn?
A. 0
B. 2
C. 3.
D. 1
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhân gốc tọa độ O làm trực tâm.
A. m = -1
B. m = 0
C. m = 1
D. m = 2
