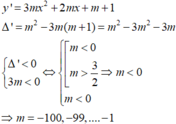Các câu hỏi tương tự
Số các giá trị nguyên của tham số m trong đoạn [-100;100] để hàm số
y
m
x
3
+
m
x
2
+
(
m
+
1
)
x
-
3
nghịch biến trên R là A. 200 B. 99 C. 100 D. 201
Đọc tiếp
Số các giá trị nguyên của tham số m trong đoạn [-100;100] để hàm số y = m x 3 + m x 2 + ( m + 1 ) x - 3 nghịch biến trên R là
A. 200
B. 99
C. 100
D. 201
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y
x
3
- 3(m-1)
x
2
+ 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S? A. S 0. B. S 1. C. S -2. D. S -1.
Đọc tiếp
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = x 3 - 3(m-1) x 2 + 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
A. S = 0.
B. S = 1.
C. S = -2.
D. S = -1.
Tìm tất cả các giá trị tham số m để hàm số
y
1
3
(
m
-
1
)
x
3
-
(
m
-
1
)
x
2
-
x
+
1
nghịch biến trên
ℝ
A.
m
≥
1
m
≤...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = 1 3 ( m - 1 ) x 3 - ( m - 1 ) x 2 - x + 1 nghịch biến trên ℝ
A. m ≥ 1 m ≤ 0
B. 0 ≤ m ≤ 1
C. m ≥ 1 m ≤ - 3
D. - 3 ≤ m ≤ 1
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số
y
3
-
x
-
3
3
-
x
-
m
nghịch biến trên khoảng (-1;1). A. 4 B. 3 C. 2 D. 0
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số y = 3 - x - 3 3 - x - m nghịch biến trên khoảng (-1;1).
A. 4
B. 3
C. 2
D. 0
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm tất cả các tham số m để hàm số
y
3
(
m
-
1
)
x
-
(
2
m
+
1
)
nghịch biến trên
ℝ
A.
2
5
≤
m
≤
4
B.
m
≤
2
5
C.
m
≤
4
D.
2
5
m
4
Đọc tiếp
Tìm tất cả các tham số m để hàm số y = 3 ( m - 1 ) x - ( 2 m + 1 ) nghịch biến trên ℝ
A. 2 5 ≤ m ≤ 4
B. m ≤ 2 5
C. m ≤ 4
D. 2 5 < m < 4
Cho hàm số
f
x
có đạo hàm trên
ℝ
thỏa mãn
f
x
+
h
-
f
x
-
h
≤
h
2
,
∀
x
∈
ℝ...
Đọc tiếp
Cho hàm số f x có đạo hàm trên ℝ thỏa mãn f x + h - f x - h ≤ h 2 , ∀ x ∈ ℝ , ∀ h > 0 .Đặt g x = x + f ' x 2019 + x + f ' x 29 - m - m 4 - 29 m 2 + 100 sin 2 x - 1 , m là tham số nguyên mà m < 27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g (x) đạt cực tiểu tại x = 0. Tính tổng bình phương các phần tử của S.
A. 108
B. 58
C. 100
D. 50
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y
m
+
1
x
3
+
m
+
1
x
2
−
2
x
+
2
nghịch biến trên
ℝ
A. 5 B. 6 C. 8 D. 7
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = m + 1 x 3 + m + 1 x 2 − 2 x + 2 nghịch biến trên ℝ
A. 5
B. 6
C. 8
D. 7
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
(
m
2
-
9
)
x
3
+
(
m
-
3
)
x
2
-
x
+
1
nghịch biến trên R A. 6 B. 4 C. 3 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = ( m 2 - 9 ) x 3 + ( m - 3 ) x 2 - x + 1 nghịch biến trên R
A. 6
B. 4
C. 3
D. 5