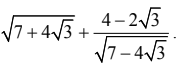4.
\(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}\right).\left(\sqrt{a}-\sqrt{b}\right)\)
\(=a-b\)
6.
\(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=1-a\)
4: Ta có: \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\cdot\left(\sqrt{a}-\sqrt{b}\right)\)
=a-b
6: Ta có: \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
=1-a