HD: Đường tròn đã cho có phương trình x2 + y2 = 8
Từ đó ta có: y = ±
Gọi S là diện tích phần tô xám ở hình bên :
và
Vậy .
c47a4970.html#ixzz43P4gPVRT
HD: Đường tròn đã cho có phương trình x2 + y2 = 8
Từ đó ta có: y = ±
Gọi S là diện tích phần tô xám ở hình bên :
và
Vậy .
c47a4970.html#ixzz43P4gPVRT
Parabol y = x 2 2 chia hai đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào trong các khoảng sau đây?
A. (0,4;0,5)
B. (0,5;0,6)
C. (0,6;0,7)
D. (0,7;0,8)
Parabol y = x 2 2 chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có diện tích là S 1 và S 2 , trong đó S 1 < S 2 . Tìm tỉ số S 1 S 2
A. 3 π + 2 21 π - 2
B. 3 π + 2 9 π - 2
C. 3 π + 2 12 π
D. 9 π - 2 3 π + 2
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , b , c = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , ( b , c ) = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Cho parabol ( P ) : y = x 2 và đường tròn (C) có tâm thuộc trục tung, bán kính bằng 1 tiếp xúc với (P) tại hai điểm phân biệt. Diện tích hình phẳng giới hạn bởi (P) và (C) (phần bôi đậm trong hình vẽ bên) bằng
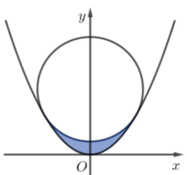
A. 14 - 3 3 - 2 π 12
B. 2 π + 3 3 - 8 12
C. 4 π - 3 3 12
D. 9 3 - 4 π 12
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
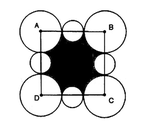
A. 5.38
B. 7.62
C. 5.98
D. 4.44
Parabol (P): y = x 2 chia đường tròn (C): x 2 + y 2 = 2 thành hai phần (tham khảo hình vẽ bên) có tỷ số diện tích (phần nhỏ chia phần lớn) bằng
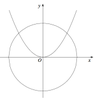
A. 3 π + 2 12 π
B. 3 π + 2 9 π - 2
C. 9 π - 2 12 π
D. 9 π - 2 18 π + 12
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S S ' để thể tích của khối nón đạt giá trị lớn nhất
A. 2 3
B. 1 4
C. 1 3
D. 6 3
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn banđầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích của khối nón đạt giá trị lớn nhất
A. 2 2
B. 1 4
C. 1 3
D. 6 3