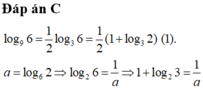Tuyển Cộng tác viên Hoc24 nhiệm kì 28 tại đây: https://forms.gle/GrfwFgzveoKLVv3p6
Các câu hỏi tương tự
Cho
f
x
a
ln
x
+
x
2
+
1
+
b
sin
x
+
6
với
a
,
b
∈
ℝ
. Biết rằng f(log(log e)) 2. Tính giá trị của f(log(ln10)). A. 10 B. 2 C. 4 D. 8
Đọc tiếp
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8
Nếu log(log(log(logx))) = 0 thì x = 10 k . Tìm giá trị của k?
A. 10
B. 100
C. 10 3
D. 10 10
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Nếu 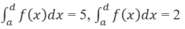
với a <d < b thì 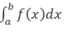
A. -2; B. 8;
C. 0; D. 3.
Nếu
∫
a
d
f
x
d
x
5
,
∫
a
d
f
x
d
x
2
v...
Đọc tiếp
Nếu ∫ a d f x d x = 5 , ∫ a d f x d x = 2 với a <d < b thì ∫ a b f x dx
A. -2; B. 8;
C. 0; D. 3.
Cho các số thực dương a,b thỏa mãn
log
a
x
,
log
b
y
. Tính
P
log
(
a
2
b
3
)
Đọc tiếp
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Nếu
log
2
10
1
a
thì log 4000 bằng A. a2 + 3 B. 4 + 2a C. 3a2 D. 3+2a
Đọc tiếp
Nếu log 2 10 = 1 a thì log 4000 bằng
A. a2 + 3
B. 4 + 2a
C. 3a2
D. 3+2a
Nếu log83 p và log35 q thì log 5 bằng: A.
1
+
3
p
q
p
+
q
B.
3
p
q
1
+
3
p
q...
Đọc tiếp
Nếu log83 = p và log35 = q thì log 5 bằng:
A. 1 + 3 p q p + q
B. 3 p q 1 + 3 p q
C. p.q
D. 3 p + q 5
Cho log a 10; log b 100. Khi đó bằng A. 290 B. 310 C. –290 D. 30
Đọc tiếp
Cho log a= 10; log b = 100. Khi đó ![]() bằng
bằng
A. 290
B. 310
C. –290
D. 30
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19