Các câu hỏi tương tự
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức
z
4
+
3
i
và số phức liên hợp của nó có điểm biểu diễn là N, N’. Biết rằng M, M’, N , N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của
z
+
4
i
−
5
.
A. ...
Đọc tiếp
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức z 4 + 3 i và số phức liên hợp của nó có điểm biểu diễn là N, N’. Biết rằng M, M’, N , N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z + 4 i − 5 .
A. 5 34 .
B. 2 5 .
C. 1 2 .
D. 4 13 .
Cho m và n là các số nguyên. Biết hàm số
y
2
x
3
+
3
1
−
m
x
2
+
6
m
−
2
x
+
n
có các cực trị đều là những số dương và một điểm cực trị
x
0
2
....
Đọc tiếp
Cho m và n là các số nguyên. Biết hàm số y = 2 x 3 + 3 1 − m x 2 + 6 m − 2 x + n có các cực trị đều là những số dương và một điểm cực trị x 0 = 2 . Tìm giá trị nhỏ nhất của m + n .
A. ‒1
B. 0
C. 8
D. 1
Cho m và n là các số nguyên. Biết hàm số y = x 3 - 6 x 2 + 9 x - 1 có các cực trị đều là những số dương và một điểm cực trị x 0 = 2 . Tìm giá trị nhỏ nhất của m + n .
A. -1
B. 0
C. 8
D. 1
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
cos
x
2
-
3
sin
x
+
c
o
s
x
trên
ℝ
. Biểu thức M + N + 2 có giá trị...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 cos x 2 - 3 sin x + c o s x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D. 2 + 3 + 2
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
−
1
+
2
c
o
s
x
2
−
3
sin
x
+
c
o
s
x
trên R. Biểu thức
M...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = − 1 + 2 c o s x 2 − 3 sin x + c o s x trên R. Biểu thức M + N + 2 có giá trị bằng:
A. 0.
B. 4 2 − 3 .
C. 2.
Hàm số y = x + 16 − x 2 có giá trị lớn nhất là M và giá trị nhỏ nhất là N . Tính tích M,N
A. 16 2 .
B.0
C.-16
D. − 16 2 .
Cho số phức z và số phức liên hợp của nó
z
có điểm biểu diễn là M, M’. Số phức
z
.
(
4
+
3
i
)
và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức
|
z
+
4
i
-
5
|
. A.
1
2...
Đọc tiếp
Cho số phức z và số phức liên hợp của nó z có điểm biểu diễn là M, M’. Số phức z . ( 4 + 3 i ) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức | z + 4 i - 5 | .
A. 1 2
B. 2 5
C. 5 34
D. 4 13
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-1;6]. Tính giá trị biểu thức
P = 2M+3N
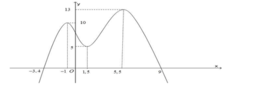
A. 8
B. 41
C. 49
D. 18
Biết rằng tồn tại các số nguyên a, b sao cho hàm số
y
a
x
+
b
x
2
+
1
đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của
a
2
+
2
b...
Đọc tiếp
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25



