Đáp án A
Ta có d 1 ∩ d 2 = A 1 ; 0 ; 2 .
Gọi vectơ đơn vị của d 1 và d 2 lần lượt là e 1 → và e 2 → ta có:

Hai vectơ chỉ phương của 2 đường phân giác lần lượt
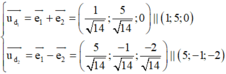
Đáp án A
Ta có d 1 ∩ d 2 = A 1 ; 0 ; 2 .
Gọi vectơ đơn vị của d 1 và d 2 lần lượt là e 1 → và e 2 → ta có:

Hai vectơ chỉ phương của 2 đường phân giác lần lượt
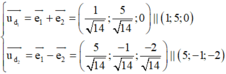
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 1 - 2 = z - 1 2 . Gọi ∆ là đường thẳng đi qua điểm A 1 ; 1 ; 1 và có véc tơ chỉ phương u → = 3 ; 4 ; 0 . Đường phân giác góc tù tạo bởi d và ∆ có phương trình là
A. x = 12 5 + 7 t y = 6 5 - t z = 2 + 5 t
B. x = 12 5 + 7 t y = 6 5 + t z = 2 + 5 t
C. x = 12 5 - 7 t y = 6 5 - t z = - 2 + 5 t
D. x = - 12 5 + 7 t y = 6 5 + t z = 2 + t
Trong không gian Oxyz cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Biết rằng u → = m ; n ; − 1 là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị của biểu thức T = m 2 + n 2
A. T = 1
B. T = 5
C. T = 2
D. T = 10
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x − 1 3 = y + 2 − 1 = z 2 . Véc tơ nào dưới đây là một véc tơ chỉ phương của d.
A. u d ⇀ = ( 1 ; − 2 ; 0 )
B. u d ⇀ = ( 2 ; 3 ; − 1 )
C. u d ⇀ = ( − 3 ; 1 ; − 2 )
D. u d ⇀ = ( 3 ; 1 ; 2 )
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x - 1 3 = y + 2 - 1 = z 2 . Véc tơ nào dưới đây là một véc tơ chỉ phương của d
A. (1; -2; 0)
B. (2; 3; -1)
C. (-3; 1; -2)
D. (3; 1; 2)
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là
A. u → = 2 ; 1 ; - 1
B. u → = 1 ; 1 ; 0
C. u → = 1 ; - 1 ; 0
D. u → = 1 ; 2 ; 1
Trong không gian O x y z , cho tam giác A B C có A 2 ; 3 ; 3 , phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng B C có một vectơ chỉ phương là
A. u → = 2 ; 1 ; − 1 .
B. u → = 1 ; 1 ; 0 .
C. u → = 1 ; − 1 ; 0 .
D. u → = 1 ; 2 ; 1 .
Trong không gian Oxyz, cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng AB có vecto chỉ phương là :
A. u 3 → 2 ; 1 ; − 2
B. u 2 → 1 ; − 1 ; 0
C. u 4 → 0 ; 1 ; − 1
D. u 1 → 1 ; 2 ; 1
Trong không gian Oxy cho điểm A 1 − ; 2 ; − 3 , véc-tơ u → 6 ; − 2 ; − 3 và đường thẳng d: x − 4 3 = y + 1 2 = z + 2 − 5 . Viết phương trình đường thẳng Δ đi qua A, vuông góc ới giá của u → và cắt d.
A. x − 1 2 = y + 1 − 3 = z − 3 6
B. x − 1 2 = y − 5 3 = z + 1 2
C. x − 1 1 = y + 4 − 3 = z − 5 4
D. x − 2 3 = y − 5 3 = z − 1 4
Trong không gian Oxyz, cho tam giác ABC với A(2;3;3), đường trung tuyến kẻ từ đỉnh B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng AB có một véctơ chỉ phương là
A. u 1 → 0 ; 1 ; - 1
B. u 2 → 2 ; 1 ; - 1
C. u 3 → 1 ; 2 ; 1
D. u 4 → 1 ; - 1 ; 0