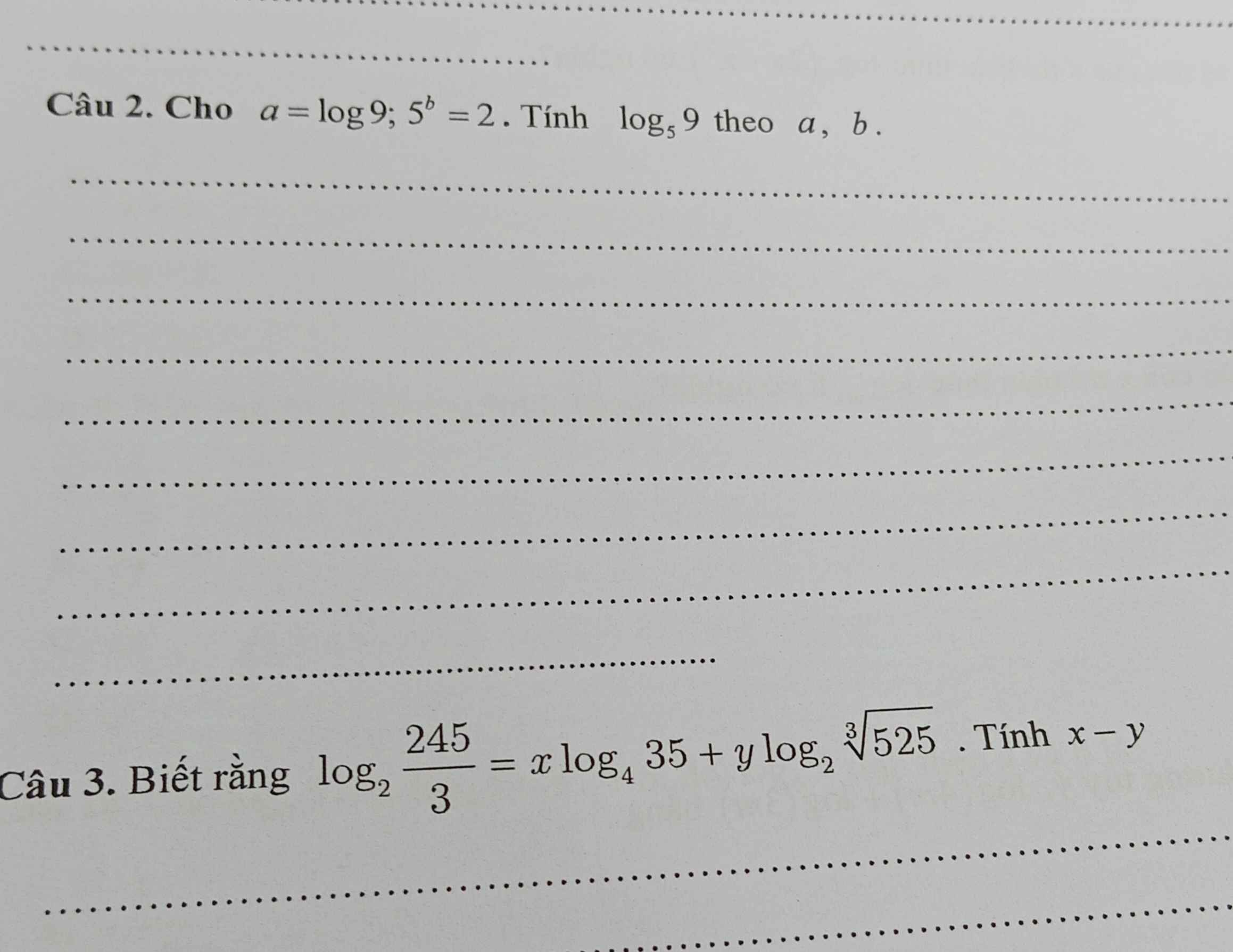Câu 2 :
\(5^b=2\Rightarrow log5^b=log2\Rightarrow log5=\dfrac{log2}{b}\)
\(log_59=\dfrac{log9}{log5}=\dfrac{a}{\dfrac{log2}{b}}=\dfrac{ab}{log2}\)
Câu 3 :
\(log_2\dfrac{245}{3}=log_2245-log_23=log_2\left(5.7^2\right)-log_23=log_25+2log_27-log_23\)
\(log_435=\dfrac{log_235}{log_24}=\dfrac{log_235}{2}=\dfrac{log_25+log_27}{2}\)
\(log_2\sqrt[3]{525}=\dfrac{1}{3}.log_2525=\dfrac{1}{3}.log_2\left(3.5.7^2\right)=\dfrac{1}{3}.\left(log_23+log_25+2log_27\right)\)
\(log_2\dfrac{245}{3}=xlog_435+y.log_2\sqrt[3]{525}\)
\(\Leftrightarrow log_25+2log_27-log_23=x.\dfrac{log_25+log_27}{2}+y.\dfrac{1}{3}.\left(log_23+log_25+2log_27\right)\)
\(\Leftrightarrow6log_25+12log_27-6log_23=3x.\left(log_25+log_27\right)+2y.\left(log_23+log_25+2log_27\right)\)
\(\Leftrightarrow6log_25+12log_27-6log_23=\left(3x+2y\right).log_25+\left(3x+4y\right).log_27+2y.log_23\)
\(\Rightarrow\left\{{}\begin{matrix}3x+2y=6\\3x+4y=12\\2y=-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-3\end{matrix}\right.\)
\(\Rightarrow x-y=4-\left(-3\right)=7\)