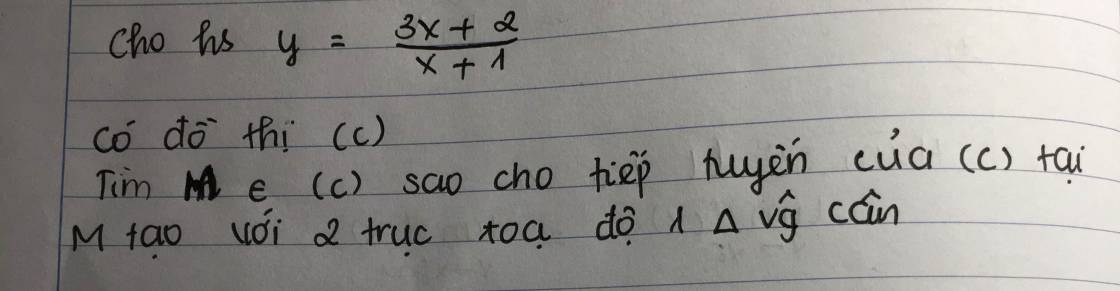`y'=[3(x+1)-3x-2]/[(x+1)^2]=1/[(x+1)^2]`
Gọi `M(x_0; y_0)-` tiếp điểm
Mà `y_0=[3x_0+2]/[x_0+1] in T T`
`=>y-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`@` Gọi `T T nn Ox =A`
`=>-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`<=>(-3x_0 -2)(x_0+1)=x-x_0`
`<=>-3x_0 ^2-3x_0 -2x_0 -2=x-x_0`
`<=>x=-3x_0 ^2-4x_0 -2`
`=>OA=|-3x_0 ^2-4x_0 -2|`
`@` Gọi `T T nn Oy=B`
`=>y-[3x_0 +2]/[x_0 +1]=1/[(x_0 +1)^2](-x_0)`
`<=>y=[(3x_0+2)(x_0+1)-x_0]/[(x_0+1)^2]`
`<=>y=[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]`
`=>OB=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
Vì `\triangle OAB` vuông cân tại `O`
`=>OA=OB`
`<=>|-3x_0 ^2-4x_0 -2|=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
`<=>(x_0+1)^2=1`
`<=>[(x_0=0),(x_0=-2):}`
`=>` PTTT: `[(y=x+2),(y=x+6):}`