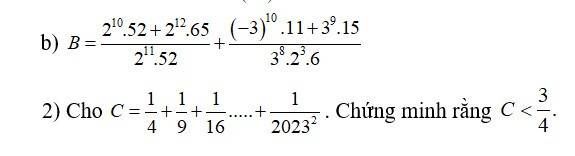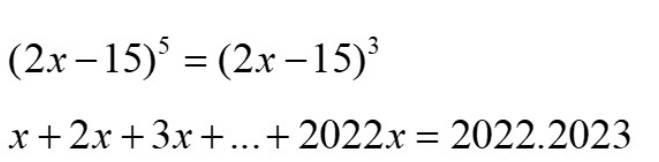Question

mik cần gấp cbn giúp me nhé ( cảm ơn )

Answer 1

b: \(=\dfrac{2^{10}\cdot2^2\cdot13+2^{12}\cdot5\cdot13}{2^{11}\cdot2^2\cdot13}+\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}\)

\(=\dfrac{2^{12}\cdot13\left(1+5\right)}{2^{13}\cdot13}+\dfrac{3^{10}\left(11+5\right)}{3^9\cdot2^4}\)

\(=\dfrac{2^{13}\cdot3}{2^{13}}+\dfrac{3^{10}\cdot16}{3^9\cdot2^4}=3+3=6\)

2: \(C=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2023^2}\)

=>\(C< \dfrac{1}{2^2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)

=>\(C< \dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{2023}=\dfrac{6065}{8092}< \dfrac{6069}{8092}=\dfrac{3}{4}\)