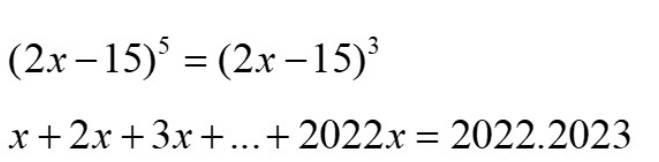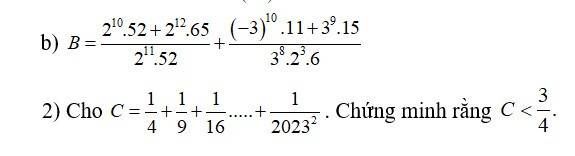\(\left(2x-15\right)^5=\left(2x-15\right)^3\)
\(\Rightarrow\left(2x-15\right)^5-\left(2x-15\right)^3=0\)
\(\Rightarrow\left(2x-15\right)^3\left[\left(2x-15\right)^2-1\right]=0\)
\(\Rightarrow\left(2x-15\right)^3\left(2x-15-1\right)\left(2x-15+1\right)=0\)
\(\Rightarrow\left(2x-15\right)^3\left(2x-16\right)\left(2x-14\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-15=0\\2x-16=0\\2x-14=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=15\\2x=16\\2x=14\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}\\x=8\\x=7\end{matrix}\right.\)
a) => (2x - 15)5 - (2x - 15)3 = 0
(2x-15)3 [(2x-15)2-1]=0
\(\Rightarrow\left[{}\begin{matrix}2x-15=0\\\left(2x-15\right)^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2x=15\\2x-15=1\\2x-15=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}\\x=8\\x=7\end{matrix}\right.\)
b) x + 2x + 3x + ... + 2022x = 2022.2023
x(1 + 2 + 3 +...+ 2022)= 2022.2023 (1)
Đặt A = 1+2+3+...+2022
Số số hạng trong A là: (2022 - 1): 1 + 1 = 2022 (số)
Tổng A bằng: \(\dfrac{\left(2022+1\right).2022}{2}=\dfrac{2022.2023}{2}\)
Thay A vào (1) , ta được:
x.\(\dfrac{2022.2023}{2}=2022.2023\)
=> x = 2
\(x+2x+3x+...+2022x=2022\cdot2023\)
\(\Rightarrow x\cdot\left(1+2+3+...+2022\right)=2022\cdot2023\)
\(\Rightarrow x\cdot\left(2022+1\right)\cdot\left[\left(2022-1\right):1+1\right]:2=2022\cdot2023\)
\(\Rightarrow x\cdot2023\cdot\left(2022-1+1\right):2=2022\cdot2023\)
\(\Rightarrow x\cdot2023\cdot2022:2=2022\cdot2023\)
\(\Rightarrow x:2=2022\cdot2023:2022\cdot2023\)
\(\Rightarrow x:2=1\)
\(\Rightarrow x=1\cdot2\)
\(\Rightarrow x=2\)