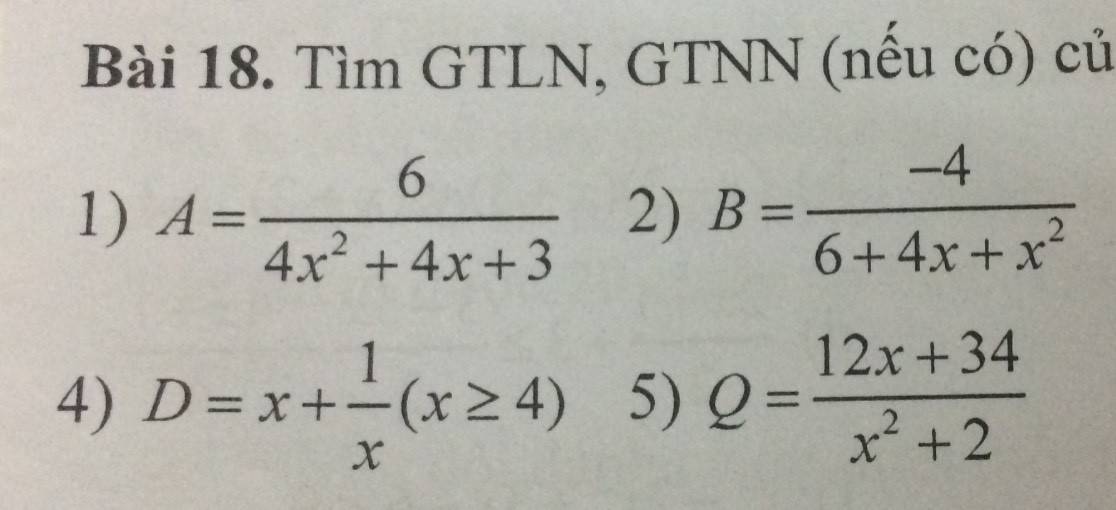c. \(\left(x+2\right)^4-6\left(x+2\right)^2+5=0\)
\(\Leftrightarrow\left(x+2\right)^4-\left(x+2\right)^2-5\left(x+2\right)^2+5=0\)
\(\Leftrightarrow\left(x+2\right)^2\left[\left(x+2\right)^2-1\right]-5\left[\left(x+2\right)^2-1\right]=0\)
\(\Leftrightarrow\left[\left(x+2\right)^2-1\right]\left[\left(x+2\right)^2-5\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+1\right)\left(x+2+\sqrt{5}\right)\left(x+2-\sqrt{5}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+1=0\\x+2+\sqrt{5}=0\\x+2-\sqrt{5}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\\x=-\sqrt{5}-2\\x=\sqrt{5}-2\end{matrix}\right.\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-3;-1;-\sqrt{5}-2;\sqrt{5}-2\right\}\)
a) \(x^{4^{ }}-x^2-2=x^4-2x^2+x^2-2=0\)
⇔\(x^4-2x^2+x^2-2=0\)
⇔\(\left(x^2-2\right)\left(x^2+1\right)=0\) nhưng x2 + 1 > 0 với mọi x vì x2 ≥ 0
⇔\(x^2-2=0\)
⇔\(x^2=2\)
⇔\(x=2^2=4\)Vậy x = 4







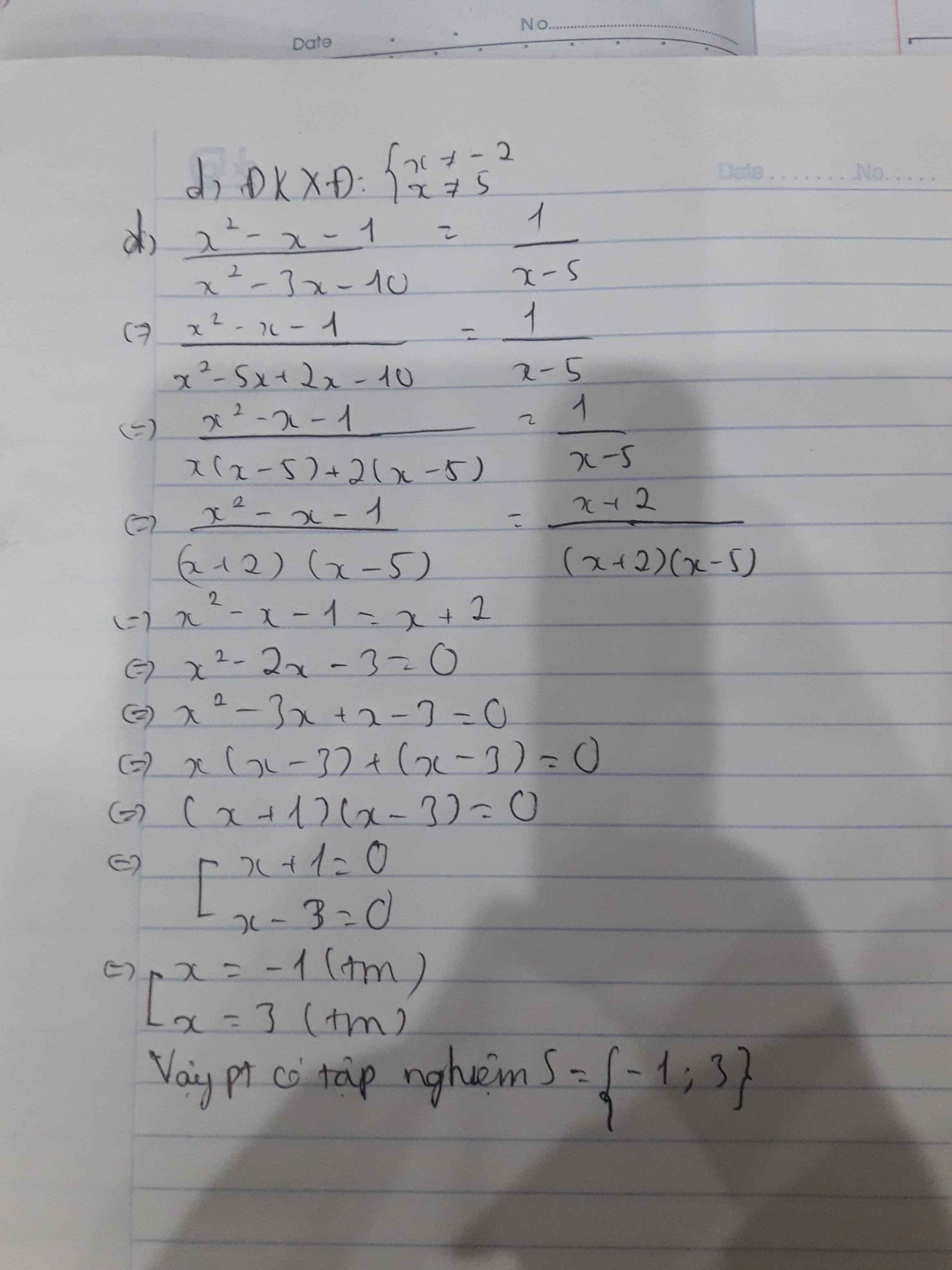




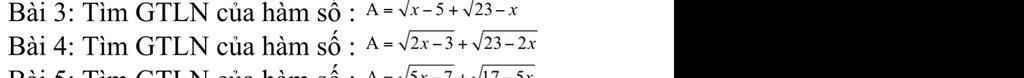



 bài 4 câu c thôi ạ
bài 4 câu c thôi ạ