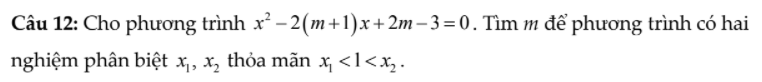\(10)\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=3\\\dfrac{3}{x}-\dfrac{2}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=6\\\dfrac{3}{x}-\dfrac{2}{y}=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x}=5\\\dfrac{1}{x}+\dfrac{1}{y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{5}=1\\1+\dfrac{1}{y}=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\dfrac{1}{y}=3-1=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(11)\left\{{}\begin{matrix}x+\dfrac{1}{y}=-\dfrac{1}{2}\\2x-\dfrac{3}{y}=-\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{2}{y}=-1\\2x-\dfrac{3}{y}=-\dfrac{7}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y}=\dfrac{5}{2}\\x+\dfrac{1}{y}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5:\dfrac{5}{2}=2\\x+\dfrac{1}{2}=-\dfrac{1}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2\\x-\dfrac{1}{2}-\dfrac{1}{2}=-1\end{matrix}\right.\)
làm bằng phương pháp thế nhé. đây là phương pháp đặt ẩn phụ ak
14: ĐKXĐ: \(y\ne-2x;y\ne\dfrac{x}{2}\)
\(\left\{{}\begin{matrix}\dfrac{1}{2x+y}+\dfrac{1}{x-2y}=\dfrac{5}{8}\\\dfrac{1}{2x+y}-\dfrac{1}{x-2y}=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2x+y}+\dfrac{1}{x-2y}+\dfrac{1}{2x+y}-\dfrac{1}{x-2y}=\dfrac{5}{8}-\dfrac{3}{8}\\\dfrac{1}{2x+y}+\dfrac{1}{x-2y}=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{2x+y}=\dfrac{2}{8}\\\dfrac{1}{x-2y}=\dfrac{5}{8}-\dfrac{1}{2x+y}=\dfrac{5}{8}-\dfrac{1}{8}=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+y=8\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y+2\\2\left(2y+2\right)+y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2y+2\\5y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4}{5}\\x=2\cdot\dfrac{4}{5}+2=\dfrac{8}{5}+2=\dfrac{18}{5}\end{matrix}\right.\left(nhận\right)\)
13: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne-1\\y\ne2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1+\dfrac{1}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{10}{x+1}-\dfrac{2}{y-2}=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{11}{x+1}=11\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\\dfrac{2}{y-2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y-2=\dfrac{2}{4}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\left(nhận\right)\)

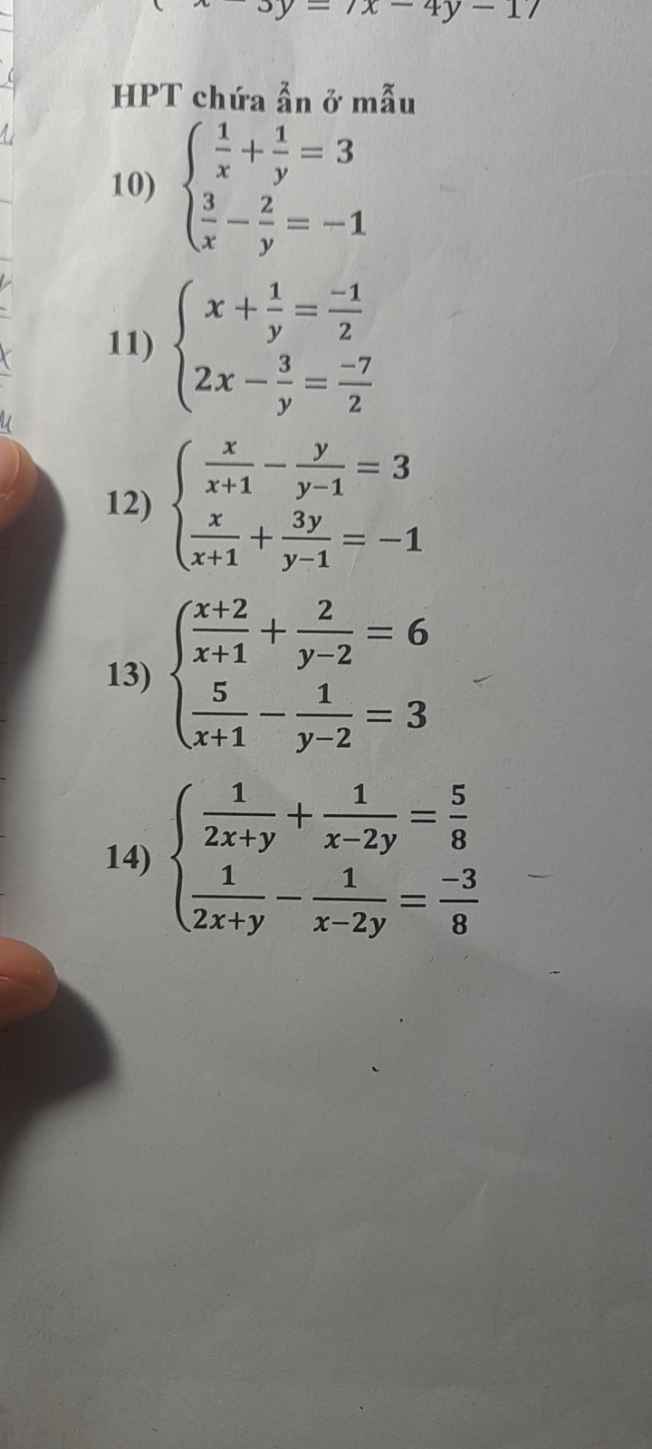 làm hộ mik nhé trừ câu 12 ra ak cảm ơn nhìu ak
làm hộ mik nhé trừ câu 12 ra ak cảm ơn nhìu ak