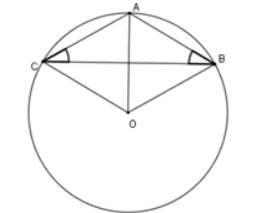
Gọi O là tâm đường tròn ngoại tiếp \(\Delta ABC\)
Vì \(\Delta ABC\) cân tại A nên \(AO\) vừa là đường cao vừa là đường phân giác của \(\widehat{BAC}\)
Suy ra: \(\widehat{CAO}=\dfrac{120}{2}=60^o\) Xét \(\Delta CAO\) có:
\(OA=OC;\widehat{CAO}=60^o\Rightarrow\) \(\Delta CAO\) là tam giác đều
nên \(OA=OC=AC=3cm\)
Nên bán kính đường tròn ngoại tiếp \(\Delta ABC\)
Là \(R=3cm\) Chu vi đường tròn \(\left(O\right)\)
Là \(C=2\pi R=6\pi\left(cm\right)\)





 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ