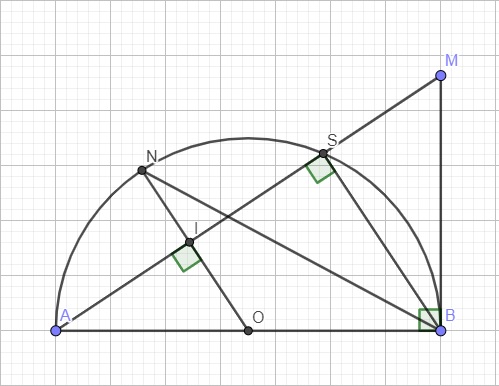
a.
Bx là tiếp tuyến \(\Rightarrow Bx\perp AB\Rightarrow\widehat{ABM}=90^0\)
\(S\in\) nửa đường tròn \(\Rightarrow\widehat{ASB}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{ASB}=90^0\)
\(\Rightarrow\widehat{ABM}=\widehat{ASB}\)
b.
Do N là điểm chính giữa cung AS \(\Rightarrow sđ\stackrel\frown{AN}=sđ\stackrel\frown{NS}\Rightarrow\widehat{ABN}=\widehat{SBN}\)
\(\Rightarrow BN\) là phân giác góc ABS
Do OB=ON=R nên \(\Delta OBN\) cân tại O \(\Rightarrow\widehat{ONB}=\widehat{OBN}\)
Mà \(\widehat{OBN}=\widehat{SBN}\left(cmt\right)\Rightarrow\widehat{ONB}=\widehat{SBN}\)
\(\Rightarrow ON||BS\) (hai góc so le trong bằng nhau)
c.
Theo cmt \(ON||BS\), mà \(BS\perp AS\Rightarrow ON\perp AS\)
\(\Rightarrow\widehat{MIO}=90^0\Rightarrow M;I;O\) cùng thuộc đường tròn đường kính OM
Theo c/m từ câu a ta có \(\widehat{MBO}=90^0\Rightarrow M;B;O\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow\) 4 điểm M;I;O;B cùng thuộc đường tròn đường kính OM hay tứ giác MIOB nội tiếp
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
