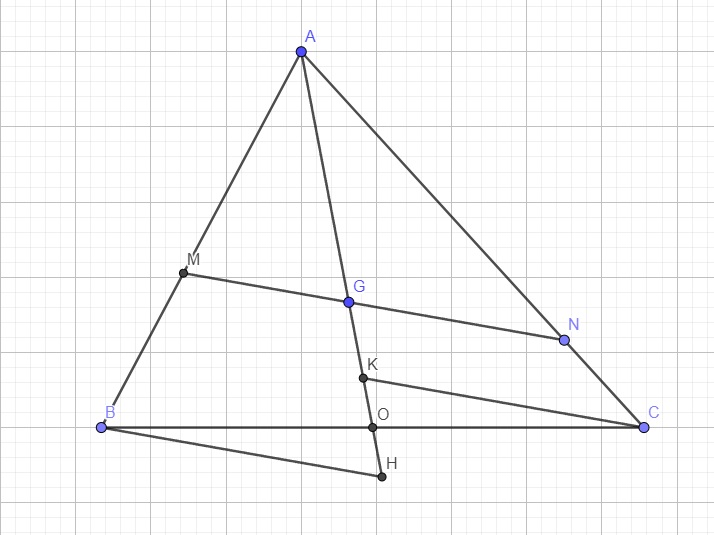
Không mất tính tổng quát, giả sử K nằm cùng phía so với A trên nửa mp bờ BC
Do BH song song MN, áp dụng định lý Thales trong tam giác ABH:
\(\dfrac{AB}{AM}=\dfrac{AH}{AG}\)
Do CK song song MN, áp dụng định lý Thales trong tam giác ACK:
\(\dfrac{AC}{AN}=\dfrac{AK}{AG}\)
Mặt khác do BH song song CK (cùng song song MN), áp dụng định lý Thales:
\(\dfrac{OH}{OK}=\dfrac{OB}{OC}=1\) (do O là trung điểm BC)
\(\Rightarrow OH=OK\)
Theo tính chất trọng tâm tam giác: \(AG=\dfrac{2}{3}AO\)
Do đó ta có:
\(\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH}{AG}+\dfrac{AK}{AG}=\dfrac{AH+AK}{AG}=\dfrac{\left(OA-OK\right)+\left(OA+OH\right)}{AG}\)
\(=\dfrac{2AO}{AG}=\dfrac{3AG}{AG}=3\)