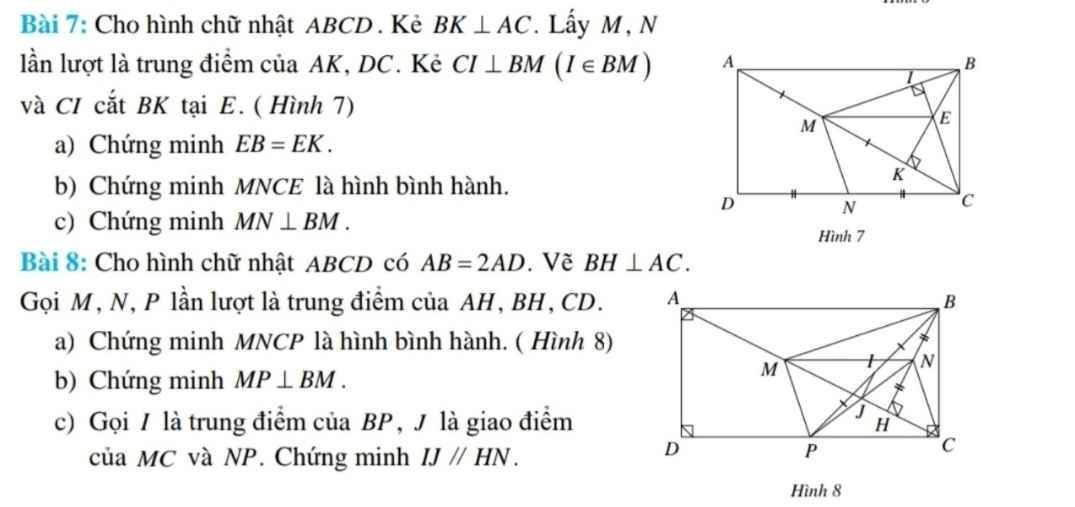
Bài 7:
a: Xét ΔBMC có
CI,BK là các đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
Ta có: ME\(\perp\)BC
AB\(\perp\)BC
Do đó: ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: Elà trung điểm của KB
=>EK=EB
b: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>ME//AB và \(ME=\dfrac{AB}{2}\)
ta có: ME//AB
AB//CD
Do đó: ME//CD
mà N\(\in\)CD
nên ME//NC
ta có: \(ME=\dfrac{AB}{2}\)
CD=AB
\(CN=\dfrac{CD}{2}\)
Do đó: ME=CN
Xét tứ giác MECN có
ME//CN
ME=CN
Do đó: MECN là hình bình hành
c: Ta có: MECN là hình bình hành
=>EC//MN
mà EC\(\perp\)BM
nên MN\(\perp\)BM
Bài 8:
Đúng 1
Bình luận (0)
