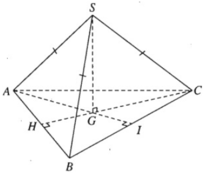
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
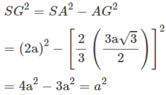
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
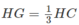
mà 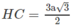
nên 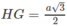

a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
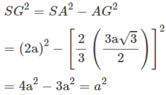
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
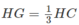
mà 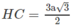
nên 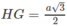
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
Hình chóp tam giác đều S. ABC ó cạnh đáy bằng 3a, cạnh bên bằng 3a. Tính khoảng cách h từ đỉnh S tới mặt phẳng đáy (ABC).
A. h = a
B. h = a 6
C. h = 3 2 a
D. h = a 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng 60 ° . Khoảng cách từ điểm S đến mặt đáy (ABC) là
![]()
![]()
![]()
![]()
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3 . Gọi O là tâm đáy ABC, d 1 là khoảng cách từ A đến mặt phẳng (SBC) và d 2 là khoảng cách từ O đến mặt phẳng (SBC). Tính d = d 1 + d 2
A. d = 2 a 2 11
B. d = 2 a 2 33
C. d = 8 a 22 33
D. d = 8 a 2 11
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o . Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
A. d = a 39 13
B. d = a 2
C. d = a
D. d = a 3
Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a 3 . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
A. a 5 2
B. 2 a 3 3
C. a 3 10
D. a 2 5
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, cạnh bên SA vuông góc
với đáy, SA=a. Tính khoảng cách từ A tới mặt phẳng (SBC).
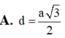
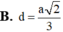
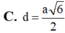
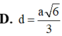
Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a 3 . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
A . a 3 10
B . 2 a 3 3
C . a 2 5
D . a 5 2