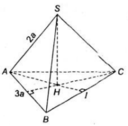
Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)
Vậy khoảng cách từ S đến (ABC ) là a.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).
b) Tính khoảng cách giữa hai đường thẳng AB và SG.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng 60 ° . Khoảng cách từ điểm S đến mặt đáy (ABC) là
Hình chóp tam giác đều S. ABC ó cạnh đáy bằng 3a, cạnh bên bằng 3a. Tính khoảng cách h từ đỉnh S tới mặt phẳng đáy (ABC).
A. h = a
B. h = a 6
C. h = 3 2 a
D. h = a 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, cạnh bên SA vuông góc
với đáy, SA=a. Tính khoảng cách từ A tới mặt phẳng (SBC).
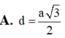
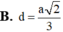
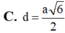
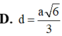
Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a 3 . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
A. a 5 2
B. 2 a 3 3
C. a 3 10
D. a 2 5
Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a 3 . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
A . a 3 10
B . 2 a 3 3
C . a 2 5
D . a 5 2
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là a 2 . Thể tích của khối nón đỉnh S đáy là đường tròn ngoại tiếp tam giác ABC bằng:
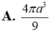
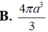
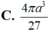
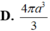
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3a,cạnh bên SC = 2a và SC vuông góc với mặt phẳng đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
A. R = 2 a 3
B. R = 3 a
C. R = a 13 2
D. R = 2 a
