Question

Hình chóp S.ABCD có đáy là hình vuông, hai mặt bên (SAB) và (SAD) vuông góc với mặt đáy. AH, AK lần lượt là đường cao của tam giác SAB, tam giác SAD. Mệnh đề nào sau đây là sai?

A. H K ⊥ S C .

B. S A ⊥ A C .

C. B C ⊥ A H .

D. A K ⊥ B D .

Answer 1

Đáp án D

Sử dụng mối quan hệ vuông góc giữa đường thẳng với đường thẳng, đường thẳng với mặt phẳng.

- Hai mặt phẳng cùng vuông góc với đường thẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó.

- Một đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó.

- Một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

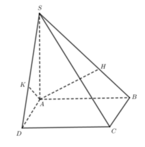
Vì   S A B ⊥ A B C D S A D ⊥ A B C D S A B ∩ S A D = S A ⇒ S A ⊥ A B C D ⇒ S A ⊥ B C

Mà A H ⊥ S B  nên A H ⊥ S B C ⇒ A H ⊥ S C .

Tương tự ta có A K ⊥ S C D ⇒ A H ⊥ S C .

Do đó S C ⊥ A H K ⇒ S C ⊥ H K ⇒ A đúng.

  S A ⊥ A B C D ⇒ S A ⊥ A C ⇒ B đúng.

  B C ⊥ A H c m t ⇒ C đúng.