Chọn D.
Phương pháp: Dùng công thức số hạng tổng quát trong khai triển nhị thức Newton.
Cách giải: Ta có:
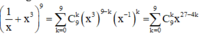

Chọn D.
Phương pháp: Dùng công thức số hạng tổng quát trong khai triển nhị thức Newton.
Cách giải: Ta có:
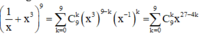

Hệ số của số hạng chứa x 3 trong khai triển 1 x + x 3 9 (với x ≠ 0 ) bằng
A. 54 x 3
B. 36
C. 126
D. 84
Cho khai triển x + 2 x 6 với x > 0 . Tìm hệ số của số hạng chứa x 3 trong khai triển trên.
A. 80
B. 160
C. 240
D. 60
Hệ số của số hạng chứa x 8 trong khai triển của biểu thức 1 x 3 - 2 x 5 12 (với x > 0) bằng
A. 59136
B. 126720
C. -59136
D. -126720
Có bao nhiêu cặp số thực (a;b) để trong khai triển ( x + a ) 3 ( x - b ) 6 , hệ số của x 7 là -9 và không có số hạng chứa x 8 .
A. 2.
B. 1.
C. 0.
D. 4.
Xét n là số nguyên dương thỏa mãn điều kiện C n + 4 n + 1 - C n + 3 n = 7 n + 3 . Hệ số của số hạng chứa x 8 trong khai triển 1 x 3 + x 5 n với x > 0, bằng
A. 549
B. 954
C. 945
D. 495
Hệ số của số hạng chứa x 8 trong khai triển câu biểu thức 1 x 3 - 2 x 5 12 (với x > 0) bằng
A.126720
B. 59136
C. -126720
D. -59136
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tìm hệ số của số hạng không chứa x trong khai triển x 2 + 4 x 18 với x ≠ 0
A. 2 9 C 18 9
B. 2 11 C 18 7
C. 2 8 C 18 8
D. 2 C 18 10 8
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525