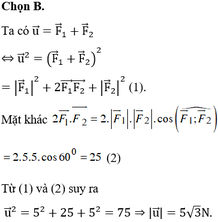Các câu hỏi tương tự
Một giá đỡ gắn vào tường như hình bên. Tam giác ABC vuông cân vuông cân tại đỉnh C. Người ta treo vào điểm A một vật nặng 5N. Cường độ hai lực tác động vào tường tại điểm B và C là
Đọc tiếp
Một giá đỡ gắn vào tường như hình bên. Tam giác ABC vuông cân vuông cân tại đỉnh C. Người ta treo vào điểm A một vật nặng 5N. Cường độ hai lực tác động vào tường tại điểm B và C là
![]()
![]()
![]()
![]()
Độ lớn F của hợp lực
F
→
của hai lực đồng quy
F
1
→
v
à
F
2
→
hợp với nhau góc α là: A.
F
F
1
2
+
F
2
2
+...
Đọc tiếp
Độ lớn F của hợp lực F → của hai lực đồng quy F 1 → v à F 2 → hợp với nhau góc α là:
A. F = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
B. F = F 1 2 + F 2 2 - 2 F 1 F 2 cos α
C. F = F 1 2 + F 2 2 + F 1 F 2 cos α
D. F = F 1 2 + F 2 2 + 2 F 1 F 2
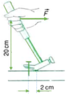
Một người dùng búa để nhổ một chiếc đinh (hình vẽ). Khi người ấy tác dụng một lực 50 N vào đầu búa thì đinh bắt đầu chuyển động. Lực cản của gỗ tác dụng vào đinh là
A. 1000 N
B. 500 N
C. 2000 N
D. 200 N
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x0 và x3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
3
là một hình chữ nhật có hai kích thước là x và
2
9
-
x
2
A. 16 B. 17 C. 19 D. 18
Đọc tiếp
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 3 là một hình chữ nhật có hai kích thước là x và 2 9 - x 2
A. 16
B. 17
C. 19
D. 18
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x0 và x3, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (
0
≤
x
≤
3
) là một hình chữ nhật có hai kích thước là x và
2
9
−
x
2
. A.
V
4
π
∫
0
3...
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ 3 ) là một hình chữ nhật có hai kích thước là x và 2 9 − x 2 .
A. V = 4 π ∫ 0 3 9 − x 2 d x
B. V = ∫ 0 3 2 x 9 − x 2 d x
C. V = 2 ∫ 0 3 x + 2 9 − x 2 d x
D. V = ∫ 0 3 x + 2 9 − x 2 d x
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x0 và x3, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (
0
≤
x
≤
3
) là một hình chữ nhật có hai kích thước là x và
2
9
−
x
2
. A.
V
4
π
∫
0
3...
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=0 và x=3, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ 3 ) là một hình chữ nhật có hai kích thước là x và 2 9 − x 2 .
A. V = 4 π ∫ 0 3 9 − x 2 d x
B. V = ∫ 0 3 2 x 9 − x 2 d x
C. V = 2 ∫ 0 3 x + 2 9 − x 2 d x
D. V = ∫ 0 3 x + 2 9 − x 2 d x
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x 1 và x 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x
1
≤
x
≤
3
thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và
3
x
2
−
2
A. ...
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1 ≤ x ≤ 3 thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 x 2 − 2
A. V = 32 + 2 15
B. V = 124 π 3
C. V = 124 3
D. V = ( 32 + 2 15 ) π
Một nguồn âm đẳng hướng đặt tại điểm O có công suất truyền âm không đổi. Mức cường độ âm tại điểm M cách O một khoảng R được tính bởi công thức
L
M
log
k
R
2
(Ben) với k là hằng số. Biết điểm thuộc đoạn thẳng AB và mức cường độ âm tại A và B lần lượt là
L
A
3
(Ben) và
L
B...
Đọc tiếp
Một nguồn âm đẳng hướng đặt tại điểm O có công suất truyền âm không đổi. Mức cường độ âm tại điểm M cách O một khoảng R được tính bởi công thức L M = log k R 2 (Ben) với k là hằng số. Biết điểm thuộc đoạn thẳng AB và mức cường độ âm tại A và B lần lượt là L A = 3 (Ben) và L B = 5 (Ben). Tính mức cường độ âm tại trung điểm AB (làm tròn đến 2 chữ số sau dấu phẩy).
A. 3,59 (Ben).
B. 3,06 (Ben).
C. 3,69 (Ben).
D. 4 (Ben).
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
.
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.
I
0
;
-...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)