Các câu hỏi tương tự
Gọi S là tổng các nghiệm phức của phương trình ( z - 1 ) 4 = 5. Tính S.
A. S = 0
B. S = 4
C. S = 2i
D. S = 4 5
Gọi S là tổng các số thực m để phương trình
z
2
-
2
z
+
1
-
m
0
có nghiệm phức thỏa mãn
z
2
Tính S.
Đọc tiếp
Gọi S là tổng các số thực m để phương trình z 2 - 2 z + 1 - m = 0 có nghiệm phức thỏa mãn z = 2 Tính S.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn |z – 1 – 2i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của |z + 2 + i|. Tính S = m2 + M2?
A. 34
B. 82
C. 68
D. 36
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
A. 6 2
B. 4 2
C. 2 2
D. 8 2
Gọi S là tổng các giá trị thực của m để phương trình 9 z 2 + 6 z + 1 - m = 0 có nghiệm phức thỏa mãn z = 1 . Tính S
A. 20
B. 12
C. 14
D. 8
Cho số phức z thỏa mãn
|
(
z
+
2
)
i
+
1
|
+
|
(
z
¯
-
2
)
i
-
1
|
10
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng SM+m.
Đọc tiếp
Cho số phức z thỏa mãn | ( z + 2 ) i + 1 | + | ( z ¯ - 2 ) i - 1 | = 10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng S=M+m.
![]()
![]()
![]()
![]()
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) 0 trên tập số phức, tính tổng: A. 2/5 B. 3/5 C. 5/4 D. 6/7
Đọc tiếp
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 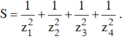
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y+2)²+ (z-3)²27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax+by-z+c0, khi đó a-b+c bằng: A. -4. B. 8. C. 0. D. 2.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y+2)²+ (z-3)²=27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax+by-z+c=0, khi đó a-b+c bằng:
A. -4.
B. 8.
C. 0.
D. 2.
Cho số phức z a +bi
(
a
,
b
∈
R
)
thỏa mãn
z
+
4
+
z
-
4
10
và
z
-
6
lớn nhất. Tính S a +b. A. S -3 B. S 5 C. S -5 D. S 11
Đọc tiếp
Cho số phức z = a +bi ( a , b ∈ R ) thỏa mãn z + 4 + z - 4 = 10 và z - 6 lớn nhất. Tính S = a +b.
A. S = -3
B. S = 5
C. S = -5
D. S = 11
Giả sử za+bi (a,b
∈
ℝ
) là số phức thỏa mãn (1+2i)z +
5
-
10
i
1
+
2
i
4. Tính tổng Sa+b
Đọc tiếp
Giả sử z=a+bi (a,b ∈ ℝ ) là số phức thỏa mãn (1+2i)z + 5 - 10 i 1 + 2 i =4. Tính tổng S=a+b
![]()
![]()
![]()
![]()



