Bài 33:
y=2x và z=2y
=>\(z=2\cdot2x=4x\)
\(\dfrac{x+y+z}{x+y-z}\)
\(=\dfrac{x+2x+4x}{x+2x-4x}\)
\(=\dfrac{7}{-1}=-7\)
Bài 34:
a: \(\dfrac{x}{x^2+x}=\dfrac{x}{x\left(x+1\right)}=\dfrac{1}{x+1}=\dfrac{\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{x+1}{x^2-1}=\dfrac{\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}=\dfrac{\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
b: \(\dfrac{x^3-1}{x^2-1};\dfrac{3}{x+1}\)
\(\dfrac{x^3-1}{x^2-1}=\dfrac{\left(x-1\right)\cdot\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+x+1}{x+1}\)
\(\dfrac{3}{x+1}=\dfrac{3}{x+1}\)
Bài 36:
a: \(\dfrac{1}{x+2}=\dfrac{1\cdot6}{6\left(x+2\right)}=\dfrac{6}{6\left(x+2\right)}\)
\(\dfrac{2}{2x+4}=\dfrac{2}{2\left(x+2\right)}=\dfrac{1}{x+2}=\dfrac{1\cdot6}{6\left(x+2\right)}=\dfrac{6}{6\left(x+2\right)}\)
\(\dfrac{3}{3x+6}=\dfrac{3}{3\left(x+2\right)}=\dfrac{1}{x+2}=\dfrac{1\cdot6}{6\left(x+2\right)}=\dfrac{6}{x+2}\)
b: \(\dfrac{1}{x+3}=\dfrac{1\cdot\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{x-3}{\left(x+3\right)\left(x-3\right)}\)
\(\dfrac{2}{2x-6}=\dfrac{2}{2\left(x-3\right)}=\dfrac{1}{x-3}=\dfrac{1\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}\)
\(\dfrac{3}{3x-9}=\dfrac{3}{3\left(x-3\right)}=\dfrac{1}{x-3}=\dfrac{1\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}\)
c: \(\dfrac{1}{x^2-4}=\dfrac{1}{\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{2}{x+2}=\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2x-4}{\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{3}{x-2}=\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x+6}{\left(x-2\right)\left(x+2\right)}\)
d: \(\dfrac{1}{x}=\dfrac{x+2}{x\left(x+2\right)}\)
\(\dfrac{2}{x+2}=\dfrac{2\cdot x}{x\left(x+2\right)}=\dfrac{2x}{x\left(x+2\right)}\)
\(\dfrac{3}{x\left(x+2\right)}=\dfrac{3}{x\left(x+2\right)}\)

 giúp mk vs ạ mik đang cần gấp
giúp mk vs ạ mik đang cần gấp 







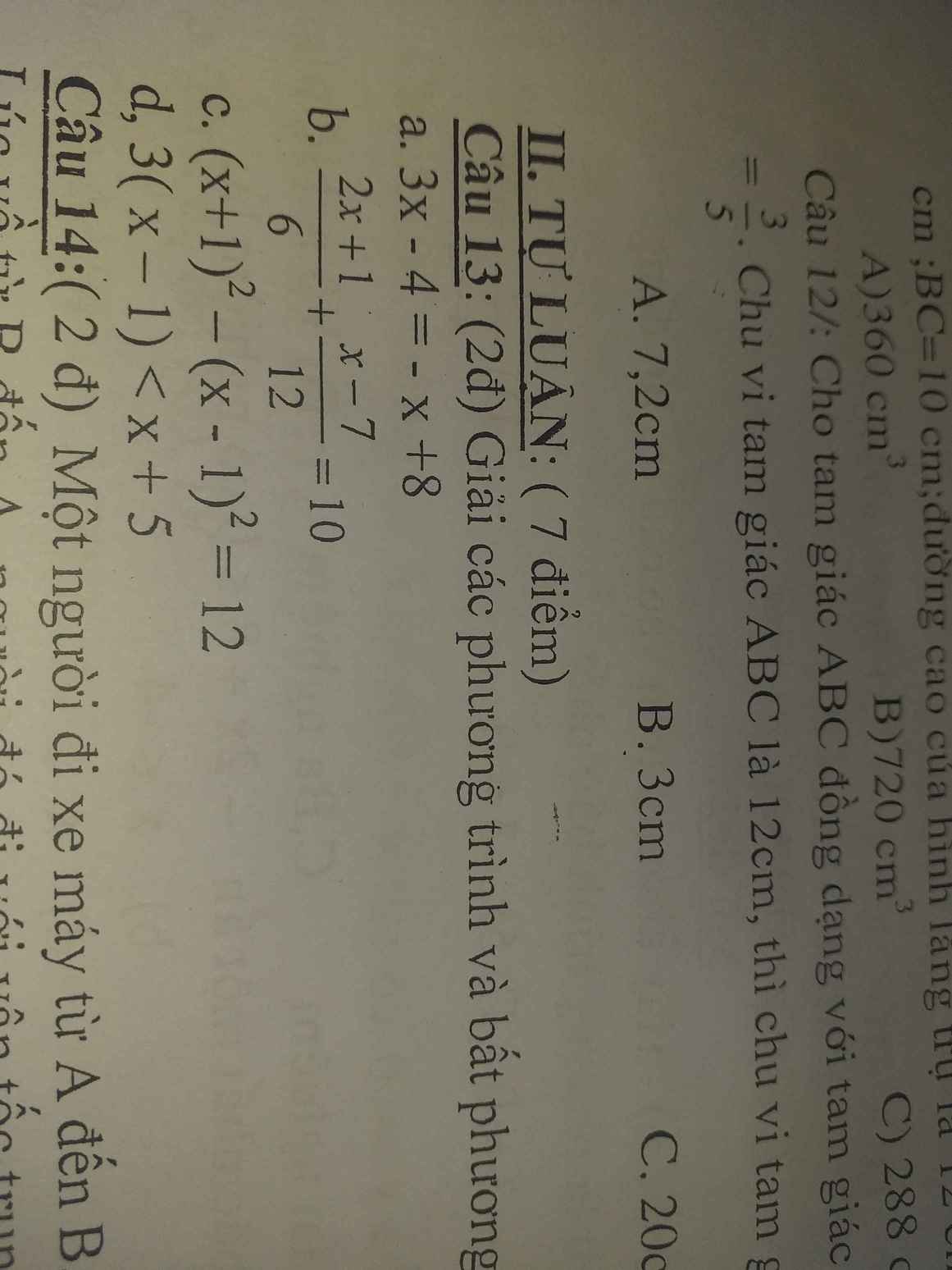





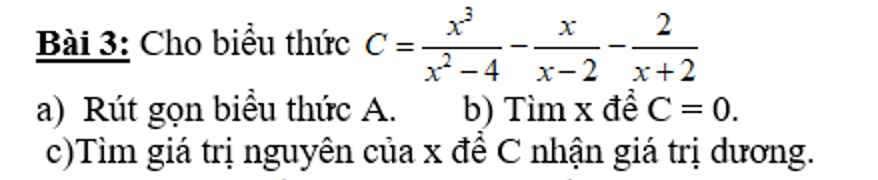


 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
