\(\text{Δ}=\left(-m\right)^2-4=m^2-4\)
Đê rphương trình có hai nghiệm thì m^2-4>=0
=>m>=2 hoặc m<=-2
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}x_1-2x_2=1\\x_1+x_2=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x_2=1-m\\x_1-2x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1-m}{-3}=\dfrac{m-1}{3}\\x_1=1+2x_2=1+\dfrac{2m-2}{3}=\dfrac{2m-2+3}{3}=\dfrac{2m+1}{3}\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=1\)
=>(m-1)(2m+1)=9
=>2m^2+m-2m-2=9
=>2m^2-m-11=0
hay \(m=\dfrac{1\pm\sqrt{89}}{4}\)






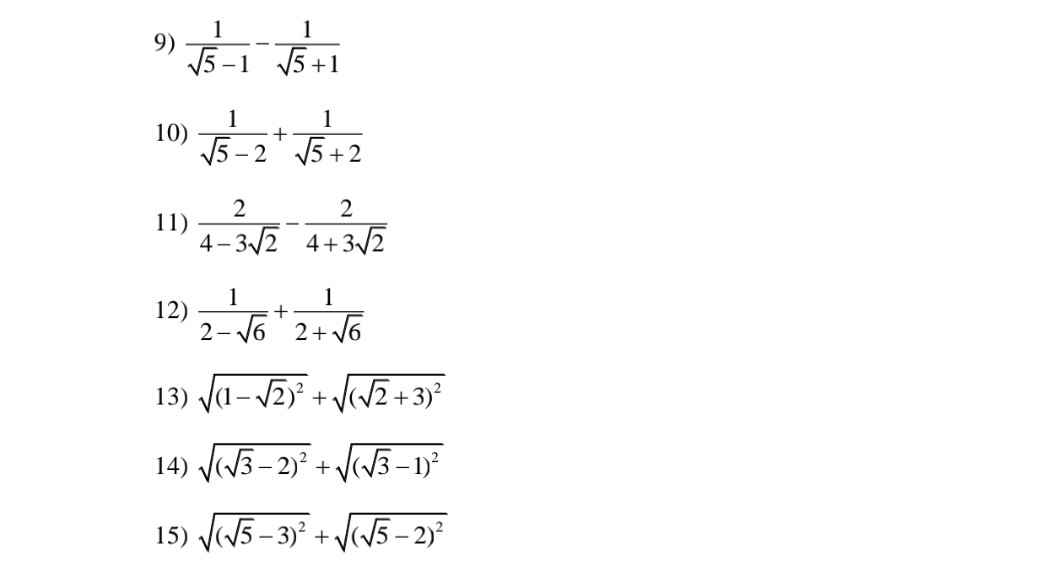












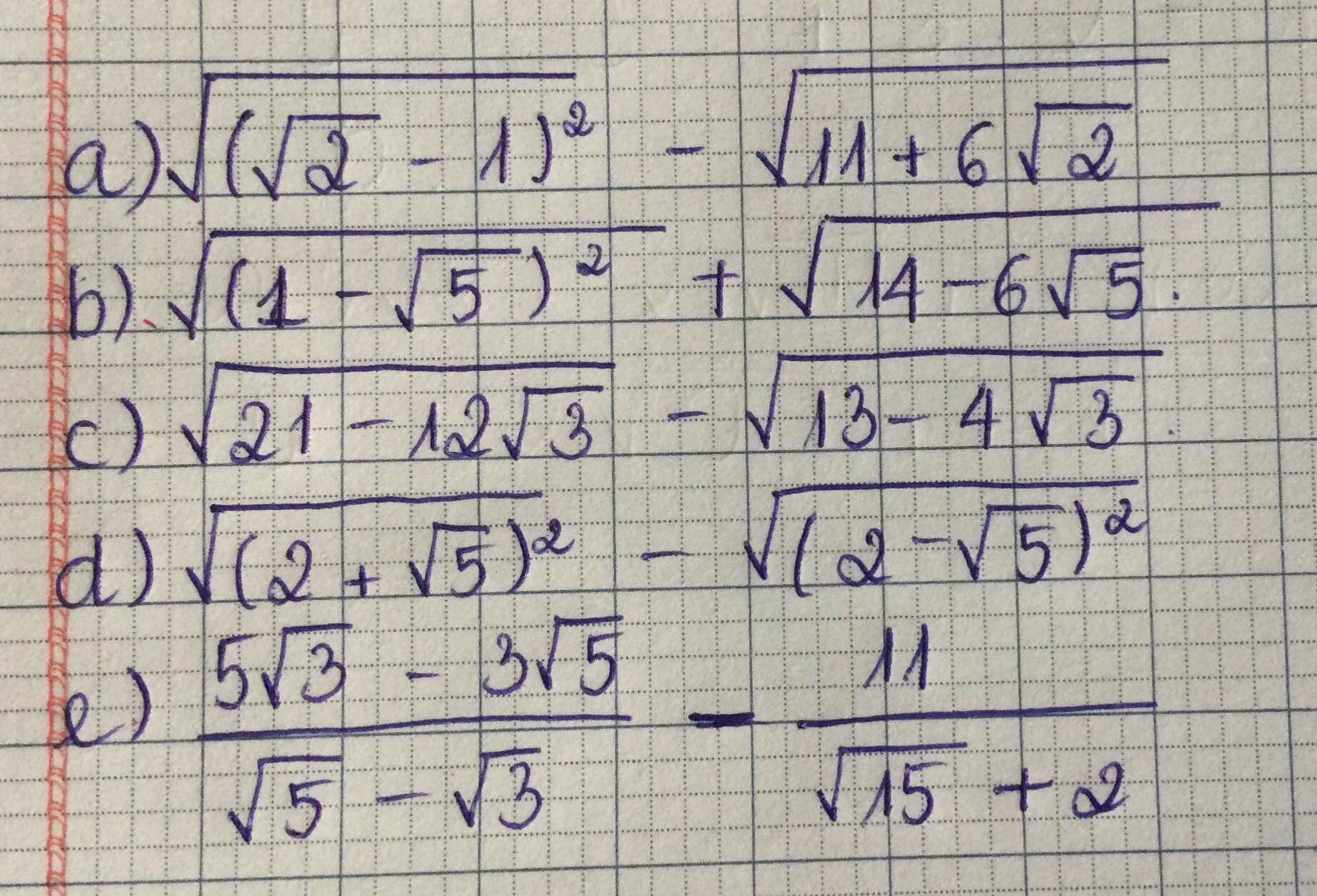 Tính và thu gọn biểu thức.
Tính và thu gọn biểu thức.