`(a):A=x(x-8)=x^{2}-8x`
`=(x^{2}-8x+16)-16`
`=(x-4)^{2}-16\ge -16` với mọi `x`
Dấu ''='' xảy ra `<=>(x-4)^{2}=0<=>x=4`
Vậy Min A `=-16<=>x=4`
`(b):\ x^{2}+x+3=(x^{2}+2.x.(1)/(2)+(1)/(4))+(11)/(4)`
`=(x+(1)/(2))^{2}+(11)/(4)\ge 11/4` với mọi `x`
`=>B=(6)/(x^{2}+x+3)\le 6:(11)/(4)=24/11`
Dấu ''='' xảy ra `<=>(x+(1)/(2))^{2}=0<=>x=-1/2`
Vậy Max B `=24/11<=>x=-1/2`
`(c):C=-x^{2}+4x+7=-(x^{2}-4x-7)`
`=-[(x^{2}-4x+4)-11]`
`=-(x-2)^{2}+11\le 11` với mọi `x`
Dấu ''='' xảy ra `<=>(x-2)^{2}=0<=>x=2`
Vậy Max `C=11<=>x=2`
`(d):D=-2x^{2}+2x-10=-2(x^{2}-x+5)`
`=-2[x^{2}-2.x.(1)/(2)+(1)/(4)+(19)/(4)]`
`=-2(x-(1)/(2))^{2}-19/2\le -19/2` với mọi `x`
Dấu ''='' xảy ra `<=>(x-(1)/(2))^{2}=0<=>x=1/2`
Vậy Max D `=-19/2<=>x=1/2`

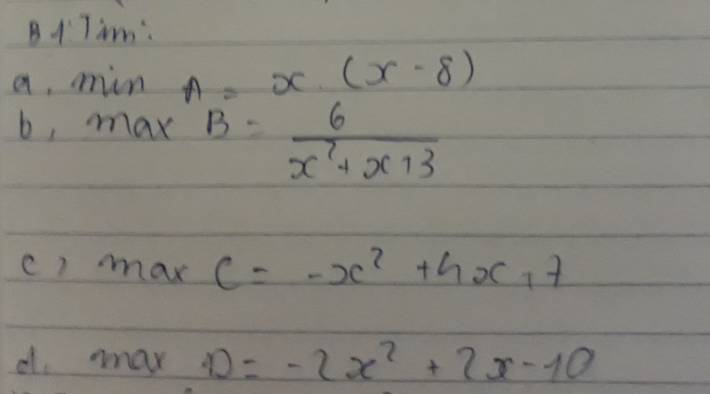

















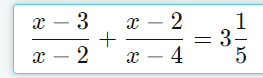 mình cần gấp giúp mình với
mình cần gấp giúp mình với