Điều kiện : \(x\in\left\{2,4\right\}\)
Biến đổi PT về dạng :
\(5\left(x-3\right)\left(x-4\right)+5\left(x-2\right)^2=16\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow5\left(x^2-7x+12\right)+5\left(x^2-4x+4\right)=16\left(x^2-6x+8\right)\)
\(\Leftrightarrow6x^2-41x+48=0\Leftrightarrow6x^2-9x-32x+48=0\)
\(\Leftrightarrow6x\left(x-\dfrac{3}{2}\right)-32\left(x-\dfrac{3}{2}\right)=0\Leftrightarrow\left(x-\dfrac{3}{2}\right)\left(6x-32\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{2}=0\\6x-32=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{16}{3}\end{matrix}\right.\)
Vậy PT có nghiệm ...
\(\Leftrightarrow\dfrac{x-3}{x-2}+\dfrac{-x-2}{x-4}=\dfrac{16}{5}\\ \Leftrightarrow\dfrac{5\left(x-3\right)\left(x-4\right)+5\left(x-2\right)^2}{5\left(x-2\right)\left(x-4\right)}=\dfrac{16\cdot\left(x-2\right)\left(x-4\right)}{5\left(x-2\right)\left(x-4\right)}\\ \Rightarrow5x^2-20x-15x+60+5x^2+20x+20=16x^2-64x-32x+128\\ \Leftrightarrow10x^2-55x+80=16x^2-96x+128\\ \Leftrightarrow6x^2-41x+48=0\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{16}{3}\\\dfrac{3}{2}\end{matrix}\right.\)

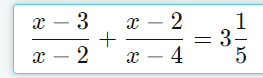 mình cần gấp giúp mình với
mình cần gấp giúp mình với