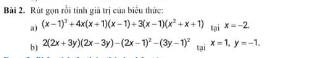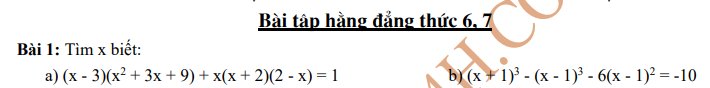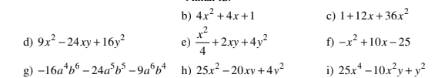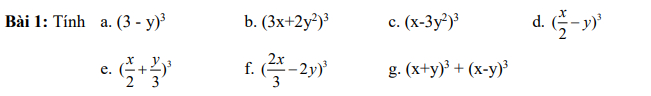a) \(\left(x-1\right)^3+4x\left(x-1\right)\left(x+1\right)+3\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3-3x^2+3x-1+4x\left(x^2-1\right)+3\left(x^3-1\right)\)
\(=x^3-3x^2+3x-1+4x^3-4x+3x^3-3\)
\(=8x^3-3x^2-x-4\)
Thay x=-2 vào biểu thức đã rút gọn ta được
\(8\left(-2\right)^3-3\left(-2\right)^2-\left(-2\right)-4=-78\)
Vậy...
b) \(2\left(2x+3y\right)\left(2x-3y\right)-\left(2x-1\right)^2-\left(3y-1\right)^2\)
\(=2\left(4x^2-9y^2\right)-\left(4x^2-4x+1\right)-\left(9y^2-6y+1\right)\)
\(=8x^2-18y^2-4x^2+4x-1-9y^2+6y-1\)
\(=4x^2+4x-27y^2+6y-2\)
Thay x=1 và y=-1 được
\(4.1+4-27.1-6-2=-27\)
Vậy...
Chụp nhỏ quá
Đúng 2
Bình luận (0)
