ĐKXĐ: x ≠ 2; x ≠ -2
Phương trình tương đương:
⇔ (1 - 6x)(x + 2) + (9x + 4)(x + 2) = x(3x - 2) + 1
⇔ x + 2 - 6x² - 12x + 9x² + 18x + 4x + 8 = 3x² - 2x + 1
⇔ 6x² + 9x² - 3x² + x - 12x + 18x + 4x + 2x = 1 - 2 - 8
⇔ 13x = -9
⇔ x = -9/13 (nhận)
Vậy S = {-9/13}
Bạn xem lại xem phương trình đã viết đúng chưa vậy?
\(\dfrac{1-6x}{x-2}+\dfrac{9x+4}{x-2}=\dfrac{x\left(3x-2\right)+1}{x^2-4}\)
\(\Leftrightarrow\dfrac{1-6x}{x-2}+\dfrac{9x+4}{x-2}=\dfrac{x\left(3x-2\right)+1}{\left(x-2\right)^2}\)
\(ĐKXĐ:x-2\ne0\\ \Leftrightarrow x\ne2\)
\(\Leftrightarrow\left(1-6x\right)\left(x-2\right)+\left(9x+4\right)\left(x-2\right)=x\left(3x-2\right)+1\)
\(\Leftrightarrow\left(x-2\right)\left(1-6x+9x+4\right)=3x^2-2x+1\)
\(\Leftrightarrow\left(x-2\right)\left(3x+5\right)-3x^2+2x-1=0\)
\(\Leftrightarrow3x^2+5x-6x-10-3x^2+2x-1=0\)
\(\Leftrightarrow x-11=0\)
\(\Leftrightarrow x=11\)(nhận)
Vậy \(S=\left\{11\right\}\)
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
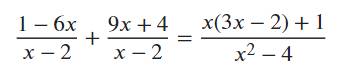
giúp mình với ạ, mình cần gấp lắm ạ
