\(1,=20x^2-15x+10x-20x^2=-5x\\ 2,=4x^2-20x+25-4x^2+18x-18=7-2x\\ 3,=\left(6x^3-4x^2-12x+8x+15x-10\right):\left(3x-2\right)\\ =\left(3x-2\right)\left(2x^2-4x+5\right):\left(3x-2\right)\\ =2x^2-4x+5\\ 4,=\dfrac{5x+25-2x+10+x^2+2x-35}{\left(x+5\right)\left(x-5\right)}=\dfrac{x\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}=\dfrac{x}{x-5}\\ 5,=\dfrac{3x-8-x-6}{x-7}+\dfrac{\left(x-2\right)\left(x+2\right)}{x-2}=\dfrac{2\left(x-7\right)}{x-7}+x+2=2+x+2=x+4\\ 6,=\dfrac{x^2+8x+16+2x-8-6x-8}{\left(x-4\right)\left(x+4\right)}=\dfrac{x\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{x}{x-4}\\ 7,=\dfrac{x\left(x-7\right)}{2x\left(x+3\right)}\cdot\dfrac{4\left(x-3\right)\left(x+3\right)}{\left(x-7\right)^2}=\dfrac{2\left(x-3\right)}{x-7}\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Giúp mình với ạ, mình đang cần gấp ạ
Giúp mình với ạ, mình đang cần gấp ạ
Giúp mình với mn ạ. Mình đang cần gấp ạ 🥺
giúp mình bài 2 với ạ mình đang cần gấp ạ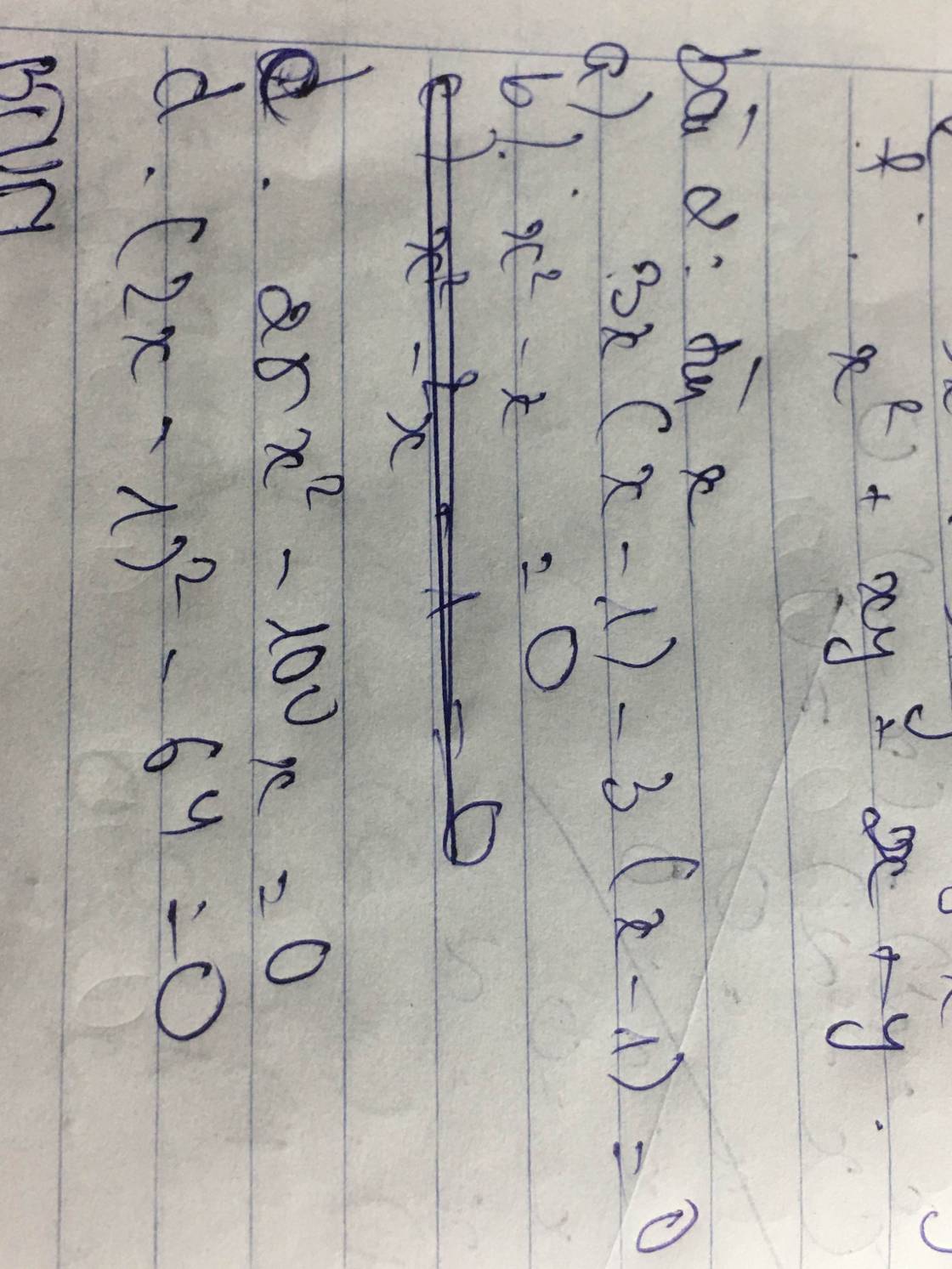
giúp mình với ạ, mình đang cần gấp 2 câu này ạ.

Giúp mình với ạ . Mình đang cần gấp 
Giúp mình với ạ mình đang cần gấp
Giúp mình với ạ,mình đang cần gấp.
giúp mình với, mình đang cần gấp ạ












