\(\dfrac{x^3}{x^2+xy+y^2}+\dfrac{y^3}{y^2+yz+z^2}+\dfrac{z^3}{z^2+zx+x^2}=\dfrac{x^3}{x^2+xz+z^2}+\dfrac{y^3}{y^2+yz+x^2}+\dfrac{z^2}{z^2+zy+y^2}\)
\(\Leftrightarrow\dfrac{x^3-y^3}{x^2+xy+y^2}+\dfrac{y^3-z^3}{y^2+yz+z^2}+\dfrac{z^3-x^3}{z^2+zx+x^2}=0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{x^2+xy+y^2}+\dfrac{\left(y-z\right)\left(y^2+yz+z^2\right)}{y^2+yz+z^2}+\dfrac{\left(z-x\right)\left(z^2+zx+x^2\right)}{z^2+zx+x^2}=0\)
\(\Leftrightarrow x-y+y-z+z-x=0\left(đúng\right)\)
Vậy ta có đpcm.

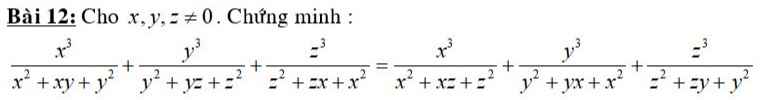













 giúp mình với ạ, mình cần gấp lắm ạ
giúp mình với ạ, mình cần gấp lắm ạ




