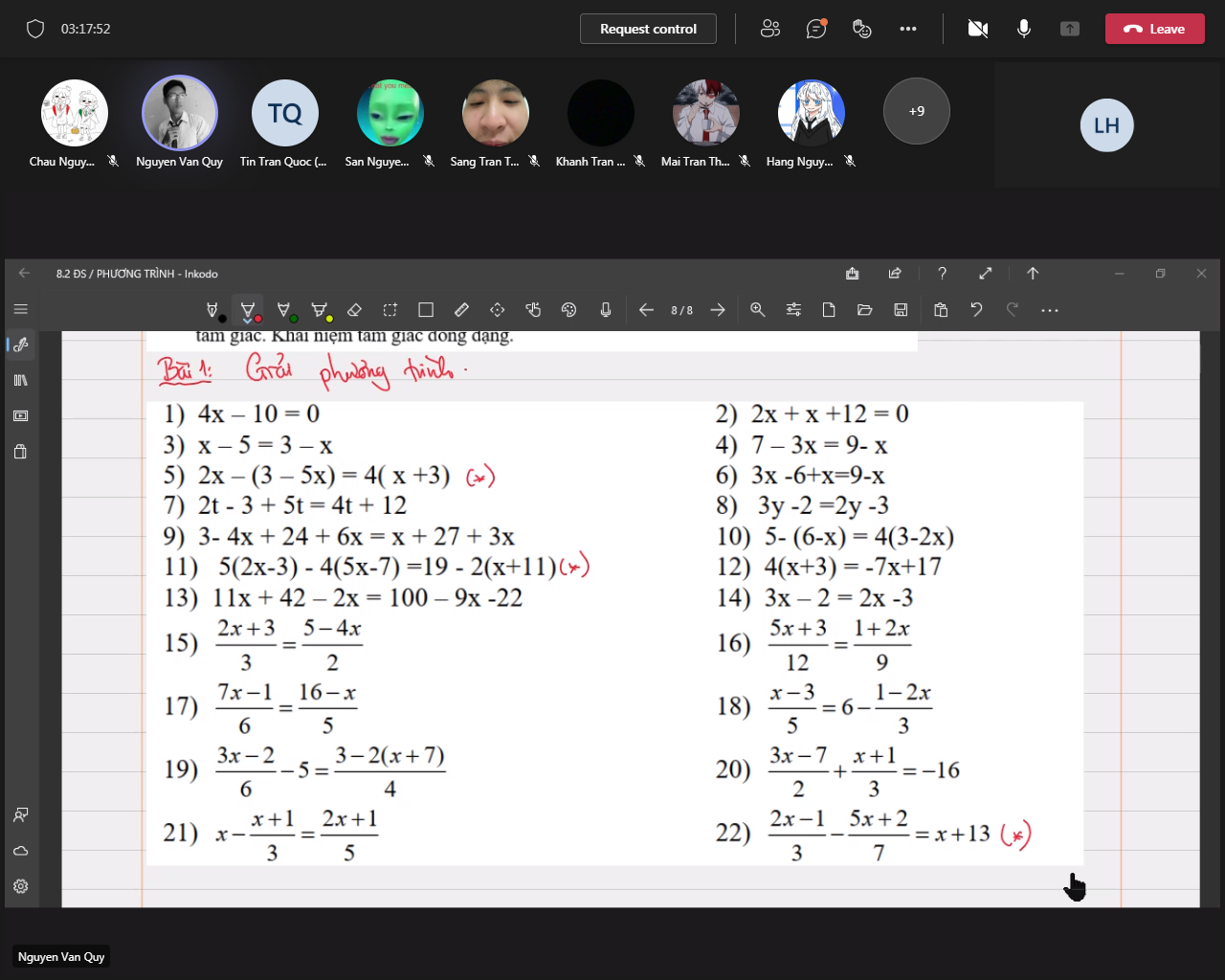
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
b: Xét tứ giác ABQC có
M là trung điểm chung của AQ và BC
=>ABQC là hình bình hành
Hình bình hành ABQC có \(\widehat{BAC}=90^0\)
nên ABQC là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét tứ giác AMBD có
E là trung điểm chung của AB và MD
=>AMBD là hình bình hành
Hình bình hành AMBD có AB\(\perp\)MD
nên AMBD là hình thoi
d: Xét ΔABC có
M,E lần lượt là trung điểm của BC,BA
=>ME là đường trung bình cuả ΔACB
=>ME//AC và \(ME=\dfrac{AC}{2}\)
Ta có: \(ME=\dfrac{AC}{2}\)
\(ME=\dfrac{MD}{2}\)
Do đó: AC=MD
Xét tứ giác ACMD có
MD//AC
MD=AC
Do đó: ACMD là hình bình hành
=>AM cắt CD tại trung điểm của mỗi đường(1)
Ta có: AEMF là hình chữ nhật
=>AM cắt EF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AM,CD,EF đồng quy
c) Ta vẽ đối xứng của M qua E và gọi điểm đó là D. Khi đó, ta có:
- MD = ME (do D là đối xứng của M qua E)
- Góc MDE = 90 độ (do ME vuông góc với AB)
Vì tam giác AEMF là hình chữ nhật (theo phần a), nên ta có:
- AE = MF
- Góc EAF = 90 độ (do AE vuông góc với AB)
- Góc MFA = 90 độ (do MF vuông góc với AC)
Do đó, ta có:
- Góc EAF = Góc MFA
- AE = MF
Khi đó, ta có tứ giác AMBD là hình thoi (do MD = ME và AB song song với DE).
d) Ta cần chứng minh rằng CD, AM, EF đồng quy. Ta có:
- AM là trung tuyến của tam giác ABC, nên AM song song với BC.
- Góc MAF = 90 độ (do ME vuông góc với AB), nên góc FAE = 90 độ - góc BAC.
- Góc MFA = 90 độ (do MF vuông góc với AC), nên góc EAF = 90 độ - góc ABC.
- Tứ giác AEMF là hình chữ nhật (theo phần a), nên AE song song với MF.
Khi đó, ta có:
- Góc FAE + góc EAF = 90 độ - góc BAC + 90 độ - góc ABC = 180 độ - (góc BAC + góc ABC) = 90 độ (do tổng hai góc BAC và ABC bằng 90 độ)
- AE song song với MF
- AM song song với BC
Do đó, ta có CD, AM, EF đồng quy.








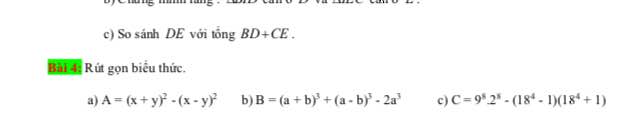

 iúp mình với câu a mình làm rồi ,chỉ làm các câu còn lại hoi
iúp mình với câu a mình làm rồi ,chỉ làm các câu còn lại hoi