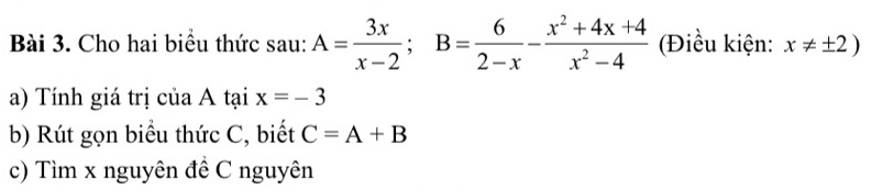\(a,A=\left(\dfrac{1}{x-2}-\dfrac{x^2+1}{4-x^2}+\dfrac{1}{1+2}\right):\dfrac{x+1}{x+2}\)
\(=\left(\dfrac{1}{x-2}+\dfrac{x^2+1}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}\right):\dfrac{x+1}{x+2}\)
\(=\left(\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2+1}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}\right):\dfrac{x+1}{x+2}\)
\(=\dfrac{x+2+x^2+1+x-2}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{x+1}\)
\(=\dfrac{x^2+2x+1}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{x+1}\)
\(=\dfrac{\left(x+1\right)^2}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{x+1}\)
\(=\dfrac{x+1}{x-2}\)
\(b,\) Ta có: \(\dfrac{x+1}{x-2}=\dfrac{x-2+3}{x-2}=\dfrac{x-2}{x-2}+\dfrac{3}{x-2}=1+\dfrac{3}{x-2}\)
Để \(A\in Z\) thì \(\dfrac{3}{x-2}\in Z\)
\(\Rightarrow x-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Vậy \(x\in\left\{3;1;5;-1\right\}\)

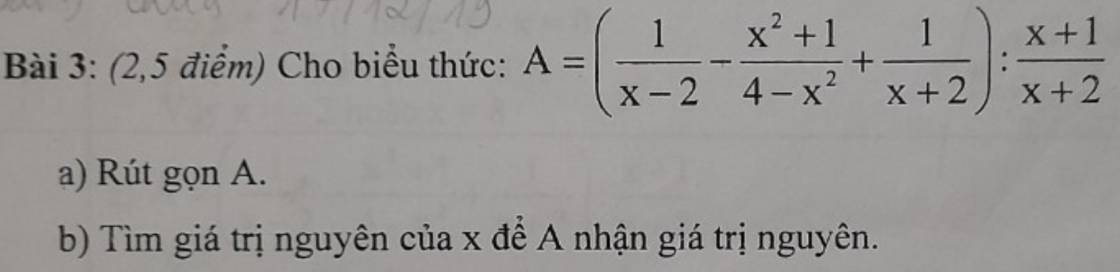






 giúp mình câu b với c với
giúp mình câu b với c với