Bài 6
a) x + 0,5 = 2/3
x + 1/2 = 2/3
x = 2/3 - 1/2
x = 1/6
b) 1/5 + (x - 2/3) = 5/3
x - 2/3 = 5/3 - 1/5
x - 2/3 = 22/15
x = 22/15 + 2/3
x = 32/15
c) (5/6 x + 3)² = 25/36
5/6 x + 3 = 5/6 hoặc 5/6 x + 3 = -5/6
*) 5/6 x + 3 = 5/6
5/6x = 5/6 - 3
5/6 x = -13/6
x = -13/6 : 5/6
x = -13/5
*) 5/6 x + 3 = -5/6
5/6 x = -5/6 - 3
5/6 x = -23/6
x = -23/6 : 5/6
x = -23/5
Vậy x = -23/5; x = -13/5
e) 2.|x - 1/8| = 6
|x - 1/8| = 6 : 2
|x - 1/8| = 3
*) Với x ≥ 1/8, ta có:
x - 1/8 = 3
x = 3 + 1/8
x = 25/8 (nhận)
*) Với x < 1/8, ta có:
x - 1/8 = -3
x = -3 + 1/8
x = -23/8 (nhận)
Vậy x = -23/8; x = 25/8
5:
2: \(\left|3x-5\right|-\dfrac{1}{7}=\dfrac{1}{3}\)
=>\(\left|3x-5\right|=\dfrac{1}{3}+\dfrac{1}{7}=\dfrac{10}{21}\)
=>\(\left[{}\begin{matrix}3x-5=\dfrac{10}{21}\\3x-5=-\dfrac{10}{21}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{115}{21}\\3x=-\dfrac{10}{21}+\dfrac{105}{21}=\dfrac{95}{21}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{115}{63}\\x=\dfrac{95}{63}\end{matrix}\right.\)
3:
\(\left(\dfrac{3}{5}x-\dfrac{2}{3}x-x\right)\cdot\dfrac{1}{7}=\dfrac{-5}{21}\)
=>\(x\left(\dfrac{3}{5}-\dfrac{2}{3}-1\right)=\dfrac{-5}{21}:\dfrac{1}{7}=\dfrac{-5}{21}\cdot7=-\dfrac{5}{3}\)
=>\(x\cdot\dfrac{9-10-15}{15}=\dfrac{-5}{3}\)
=>\(x\cdot\dfrac{-16}{15}=\dfrac{-5}{3}\)
=>\(x=\dfrac{5}{3}:\dfrac{16}{15}=\dfrac{5}{3}\cdot\dfrac{15}{16}=\dfrac{75}{48}=\dfrac{25}{16}\)
5:
\(0,2+\left|x-2,3\right|=1,1\)
=>\(\left|x-2,3\right|=1,1-0,2=0,9\)
=>\(\left[{}\begin{matrix}x-2,3=0,9\\x-2,3=-0,9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2,3+0,9=3,2\\x=2,3-0,9=1,4\end{matrix}\right.\)
6: \(5\left(x+2\right)^3+7=2\)
=>\(5\left(x+2\right)^3=-5\)
=>\(\left(x+2\right)^3=-1\)
=>x+2=-1
=>x=-3
8: \(14-\left|\dfrac{3}{2}x-1\right|=9\)
=>\(\left|\dfrac{3}{2}x-1\right|=14-9=5\)
=>\(\left[{}\begin{matrix}\dfrac{3}{2}x-1=5\\\dfrac{3}{2}x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{2}x=6\\\dfrac{3}{2}x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=6:\dfrac{3}{2}=6\cdot\dfrac{2}{3}=4\\x=-4:\dfrac{3}{2}=-4\cdot\dfrac{2}{3}=-\dfrac{8}{3}\end{matrix}\right.\)








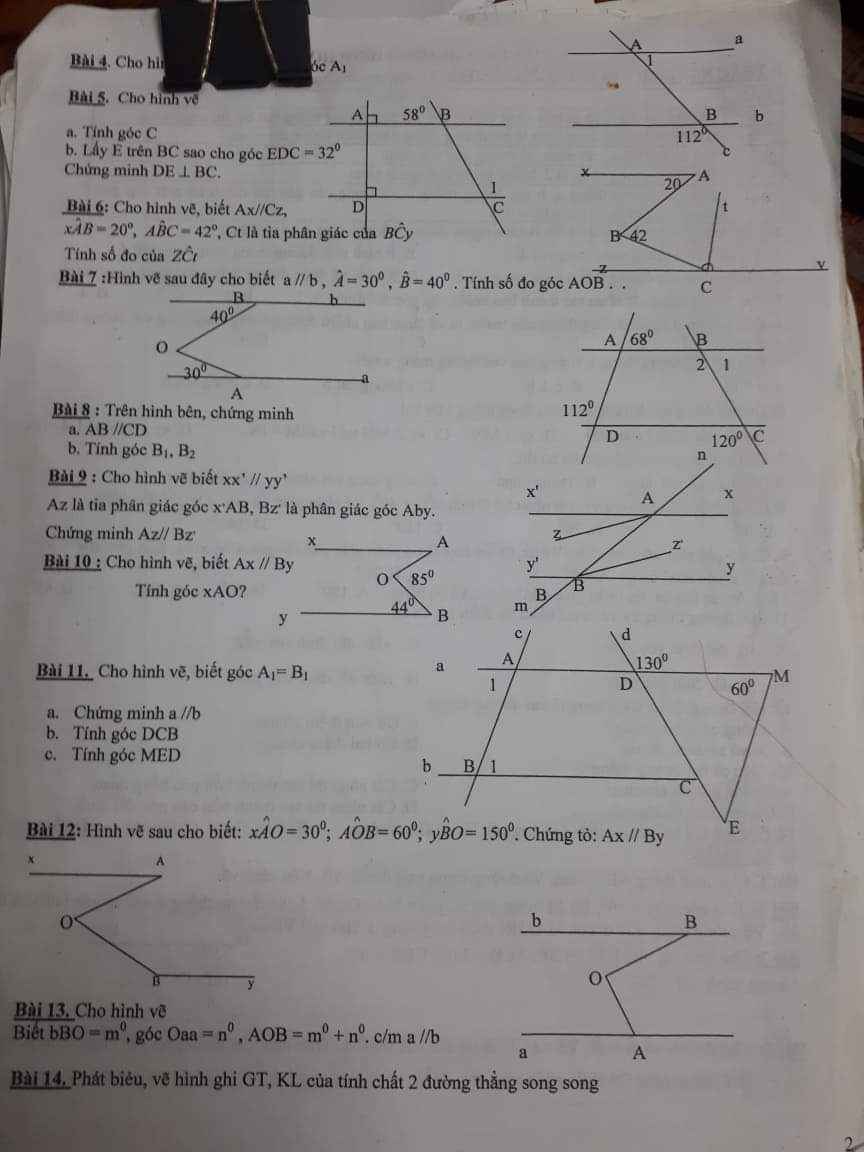




 helppppp
helppppp
