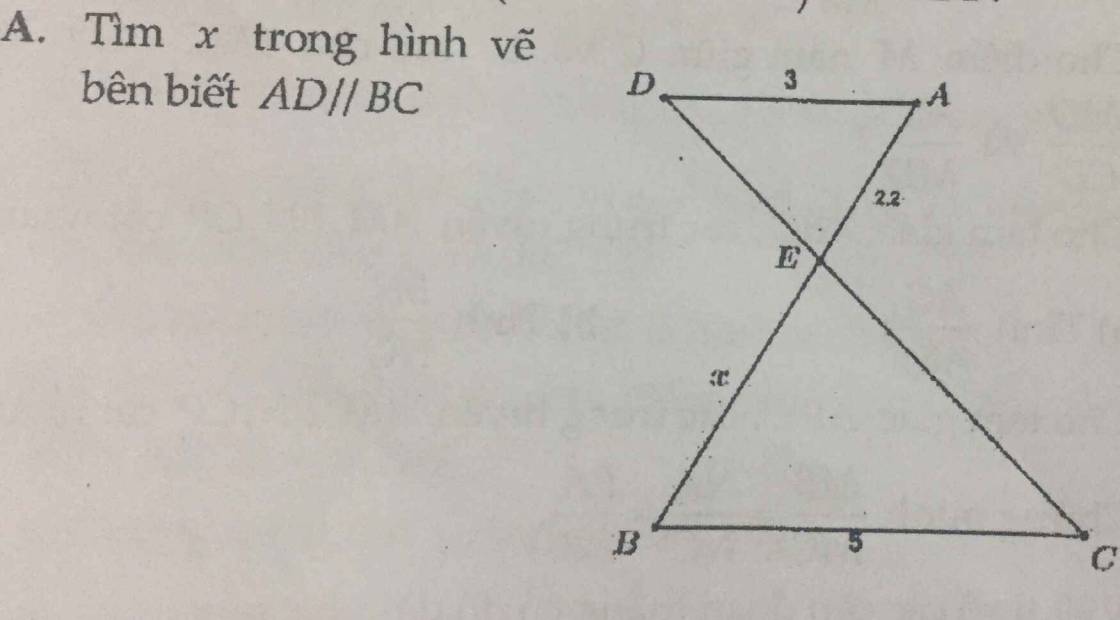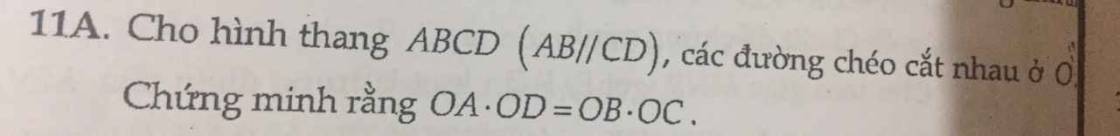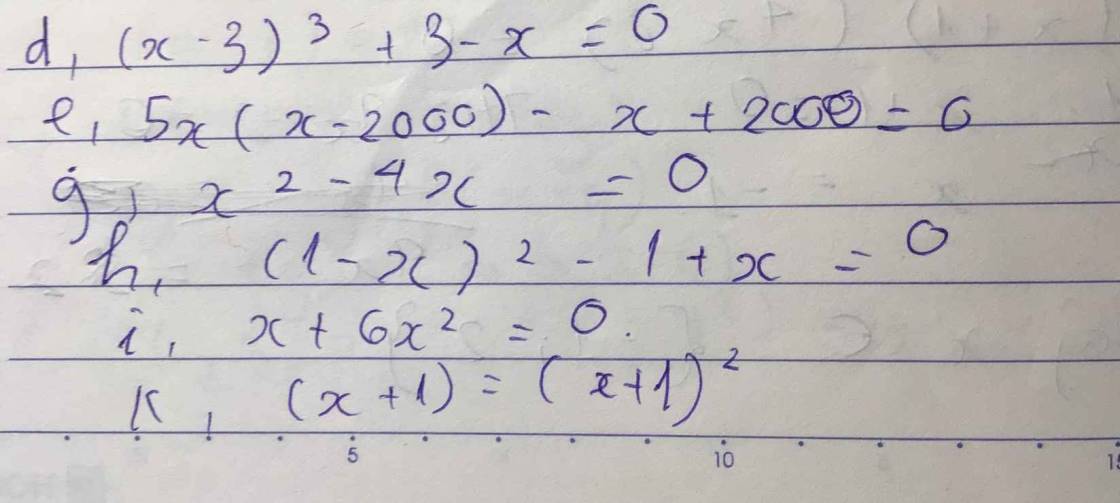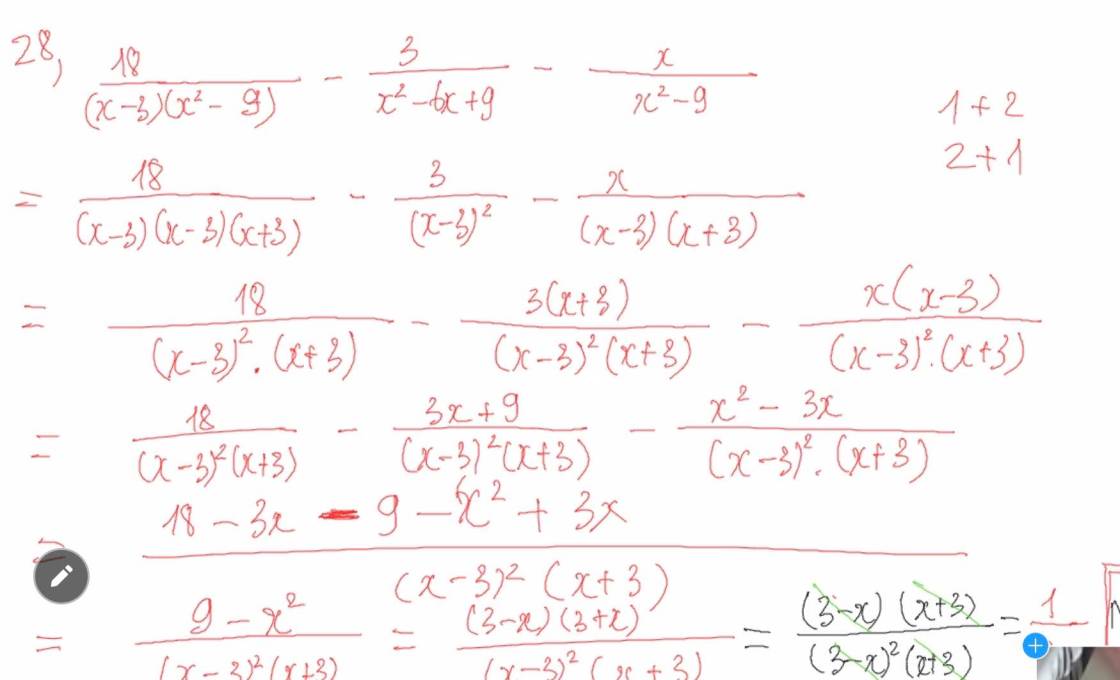11A:
Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔOAB đồng dạng với ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(OA\cdot OD=OB\cdot OC\)
9A:
a: MK//AD
=>\(\widehat{CKM}=\widehat{CAD}\)
mà \(\widehat{CKM}=\widehat{AKE}\)(hai góc đối đỉnh)
nên \(\widehat{AKE}=\widehat{CAD}\left(1\right)\)
AD//EM
=>\(\widehat{BAD}=\widehat{AEK}\)(hai góc đồng vị)(2)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{AKE}=\widehat{AEK}\)
=>ΔAEK cân tại A
=>AK=AE
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{BA}{CA}\)
Xét ΔBME có AD//ME
nên \(\dfrac{BA}{BE}=\dfrac{BD}{BM}\)
Xét ΔCAD có MK//AD
nên \(\dfrac{CM}{CD}=\dfrac{CK}{CA}\)
\(\dfrac{BA}{BE}\cdot\dfrac{CK}{CA}=\dfrac{BD}{CM}\cdot\dfrac{CM}{CD}=\dfrac{BD}{CD}\)
=>\(\dfrac{BA}{CA}\cdot\dfrac{CK}{BE}=\dfrac{BA}{CA}\)
=>\(\dfrac{CK}{BE}=1\)
=>CK=BE