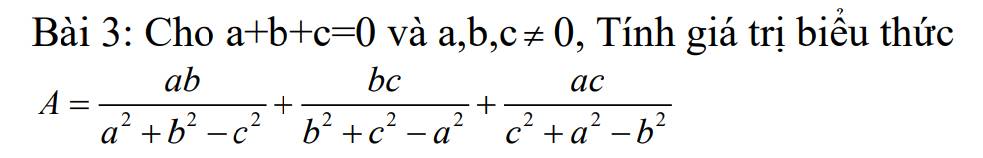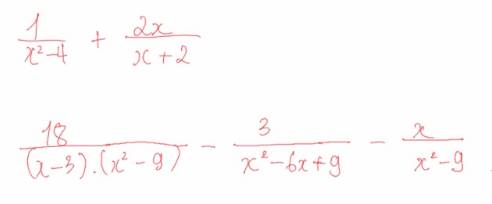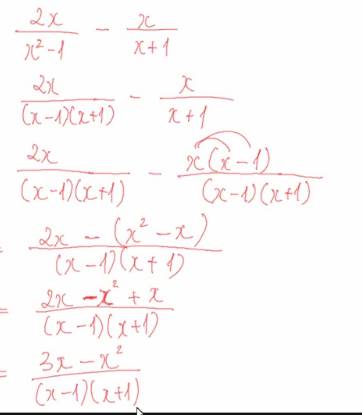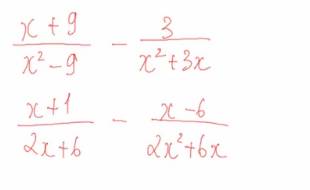Ta có:
\(a^2+b^2-c^2=\left(a+b\right)^2-c^2-2ab=\left(a+b+c\right)\left(a+b-c\right)-2ab=0-2ab=-2ab\)
Tương tự: \(b^2+c^2-a^2=-2bc\)
\(c^2+a^2-b^2=-2ca\)
\(\Rightarrow A=\dfrac{ab}{-2ab}+\dfrac{bc}{-2bc}+\dfrac{ac}{-2ca}\\ =-\dfrac{1}{2}+\left(-\dfrac{1}{2}\right)+\left(-\dfrac{1}{2}\right)=-\dfrac{3}{2}\)