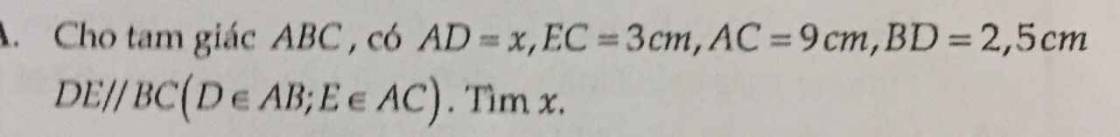5B:
AE+EC=AC
=>AE+4,5=9,5
=>AE=5(cm)
Xét ΔABC có DE//BC
nên \(\dfrac{AE}{EC}=\dfrac{AD}{DB}\)
=>\(\dfrac{8}{DB}=\dfrac{5}{4,5}=\dfrac{10}{9}\)
=>\(DB=8\cdot\dfrac{9}{10}=7,2\left(cm\right)\)
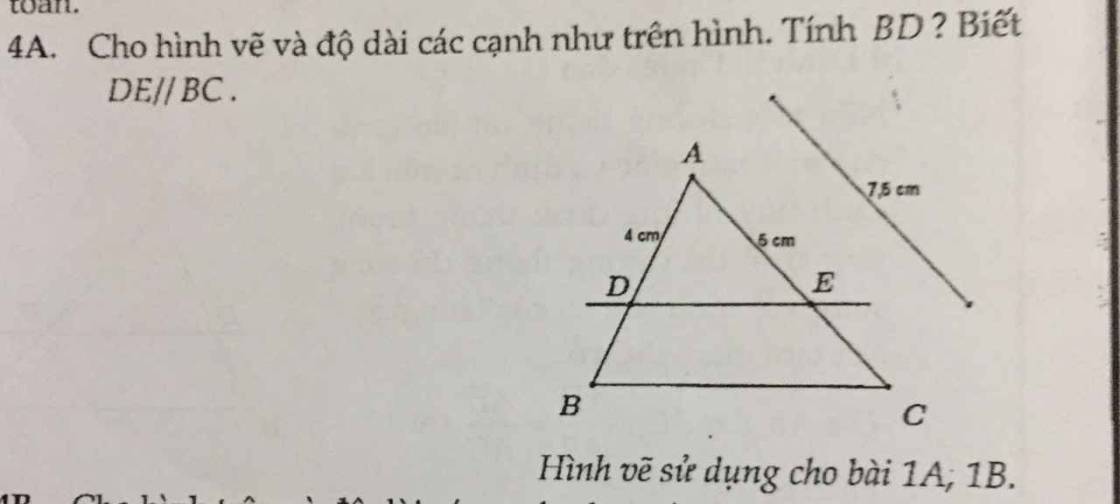
4A:
Xét ΔABC có DE//BC
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(\dfrac{4}{AB}=\dfrac{5}{7,5}=\dfrac{2}{3}\)
=>\(AB=4\cdot\dfrac{3}{2}=6\left(cm\right)\)
AD+DB=AB
=>DB+4=6
=>DB=2(cm)
1A:
a: M là trung điểm của AB
=>\(MA=MB=\dfrac{AB}{2}\)
=>\(\dfrac{MA}{MB}=1\)
b: MA=AB/2
=>\(\dfrac{MA}{AB}=\dfrac{1}{2}\)
2A:
a: Xét ΔABC có
AM,BN,CP là các đường trung tuyến
AM,BN,CP đồng quy tại G
Do đó: G là trọng tâm của ΔABC
=>\(AG=\dfrac{2}{3}AM\)
=>\(\dfrac{AG}{AM}=\dfrac{2}{3}\)
b: Xét ΔBCA có
G là trọng tâm
BN là đường trung tuyến
Do đó: \(BG=\dfrac{2}{3}BN\)
BG+GN=BN
=>\(\dfrac{2}{3}BN+GN=BN\)
=>\(GN=\dfrac{1}{3}BN\)
=>\(\dfrac{BN}{NG}=3\)