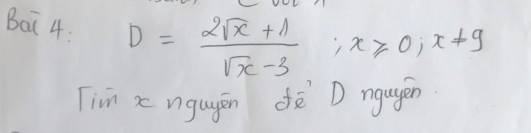\(D=\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{2\left(\sqrt{x}-3\right)+7}{\sqrt{x}-3}=2+\dfrac{7}{\sqrt{x}-3}\left(x\ge0;x\ne9\right)\)
Để \(D\) nguyên thì \(2+\dfrac{7}{\sqrt{x}-3}\) nguyên
\(\Rightarrow \dfrac{7}{\sqrt x-3}\) nguyên
\(\Rightarrow7⋮\sqrt{x}-3\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(7\right)\)
\(\Rightarrow\sqrt{x}-3\in\left\{1;7;-1;-7\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{4;10;2;-3\right\}\) mà \(\sqrt{x}\ge0\)
\(\Rightarrow\sqrt{x}\in\left\{4;10;2\right\}\)
\(\Rightarrow x\in\left\{16;100;4\right\}\left(tm.đk.x.nguyên\right)\)
Kết hợp với điều kiện, ta được: \(x\in\left\{4;16;100\right\}\)
\(D=\dfrac{2\sqrt[]{x}+1}{\sqrt[]{x}-3}\in Z\left(x\ge0;x\ne9\right)\)
\(\Leftrightarrow2\sqrt[]{x}+1⋮\sqrt[]{x}-3\)
\(\Leftrightarrow2\sqrt[]{x}+1-2\left(\sqrt[]{x}-3\right)⋮\sqrt[]{x}-3\)
\(\Leftrightarrow2\sqrt[]{x}+1-2\sqrt[]{x}+6⋮\sqrt[]{x}-3\)
\(\Leftrightarrow7⋮\sqrt[]{x}-3\)
\(\Leftrightarrow\sqrt[]{x}-3\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{4;16;100\right\}\)